Inhoudsopgave
SchakelMeting van de normale lengte bij tandwielinspectiemethoden
Als we het hebben over inspectiemethoden voor tandwielen, dan is het meten van de lengte van de gewone normale lijn een eenvoudige en kosteneffectieve techniek die veel gebruikt wordt bij de productie van tandwielen en reverse engineering-inspecties. .
Deze methode, in vergelijking met de traditionele meting van de individuele tanddikte, vereenvoudigt niet alleen de bewerking, maar voorkomt ook effectief problemen gerelateerd aan lokale elastische vervorming veroorzaakt door puntcontact, waardoor de nauwkeurigheid van de metingen toeneemt. Bij het meten met kettingtand noniuskalibers voor tanddikte is het essentieel om ervoor te zorgen dat de kalibers parallel blijven aan het tandoppervlak, waardoor de meting ongetwijfeld moeilijker wordt. Bovendien is het gebruik van CNC-apparatuur (Computer Numerical Control) voor metingen weliswaar nauwkeurig, maar ook duur en omslachtig.
Dit artikel zal beginnen met een introductie van het basisconcept van de involute lijn, waarbij geleidelijk dieper wordt ingegaan op het concept van de gear's common normal. Aan het einde van dit artikel zou je er een uitgebreid begrip van moeten hebben en in staat moeten zijn om deze kennis effectief toe te passen in je werk.
Het basisconcept van Involute
Inleiding tot Involute: vereenvoudigd begrip en basiskennis
De involuut, een concept dat vaak wordt genoemd in wiskunde en techniek, kan worden begrepen aan de hand van een eenvoudig experiment: stel je voor dat we een niet-elastisch dun touwtje om een cirkelvormig object wikkelen (zie het als een perfecte cirkel). Als we dit touwtje langzaam beginnen af te rollen terwijl we het strak houden, vormt het pad dat het uiteinde van het touwtje aflegt een zogenaamde involuut. In dit proces wordt het cirkelvormige object de “basiscirkel” genoemd en de afrollende snaar de “genererende lijn”.”

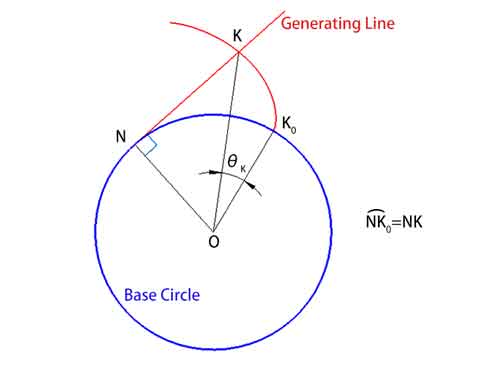
In deze actie blijft degenererende lijn tangent aan de basiscirkel, en in elk punt op de involute staat hij loodrecht op de kromme. Deze hoek, die we de afwikkelhoek θ (∠KOK0) noemen, is de hoek die gevormd wordt door de lijn die het punt op de involute (K) met het middelpunt van de basiscirkel (O) verbindt vanaf het beginpunt van de involute (K0) .
Omdat de lengte van de snaar niet verandert, zijn de booglengte op de basiscirkel (boog NK0) en de lengte van de voortbrengende lijn (NK) numeriek gelijk.
Het begrip drukhoek α en de veranderlijkheid ervan
Laten we dieper ingaan op een concept dat nauw verwant is aan de spiraal: de drukhoek α. De drukhoek is de hoek tussen de normaal in een willekeurig punt op de spiraal (de lijn loodrecht op de spiraal) en de snelheidsrichting door dat punt. Het is belangrijk op te merken dat de drukhoek op elk punt langs de spiraal varieert, beginnend bij nul aan het begin van de spiraal en geleidelijk toenemend naarmate deze naar buiten beweegt.
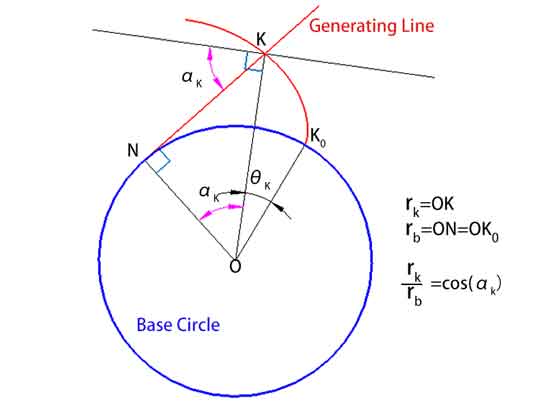
Bovendien kan de afstand van een punt K op de spiraal tot het middelpunt van de cirkel, rk, worden berekend met de formule rk = rb / cos(αk), waarbij rb de straal van de basiscirkel is en αk de drukhoek in punt K is.
Normale functie
Het functionele verband tussen de afwikkelhoek θ en de drukhoek α wordt de involutiefunctie genoemd, aangeduid met inv(α).
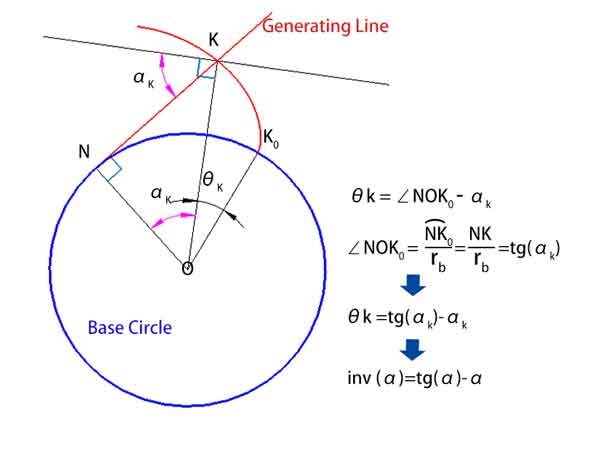
Zoals weergegeven in het diagram hieronder, θk = ∠NOK0 - αk
Waarbij de ∠NOK0 gelijk is aan debooglengte NK0 gedeeld door de straal rb, gemeten in booglengte-eenheden, die ook kunnen worden omgezet naar graden.
Omdat de booglengte NK0 = NK, dus = NK / rb = tg(αk).
We hebben dus θk = tg(αk) - αk
Dat betekent inv(αk) = tg(αk) - αk.
Het concept van het gangbare normaal van de versnelling
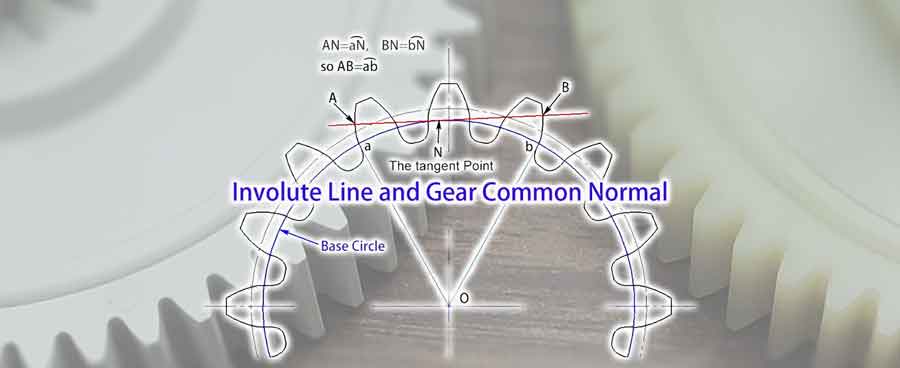
Nu we het basisconcept van de involute hebben begrepen, kunnen we ons verdiepen in het concept van de gemeenschappelijke normaal van het tandwiel. Deze verwijst naar elke tangente lijn op de basiscirkel die de tandwielprofielen snijdt op punten gescheiden door meerdere tanden. Door de eigenschappen van de involute weten we dat deze lijn loodrecht staat op de involuten die deze twee tandwielprofielen vormen.
Uit illustraties kunnen we opmaken dat de llengte van de gemeenschappelijke normaal (AB), genesteld tussen deze twee tandwielprofielen, gelijk is aan de booglengteab op de basiscirkel. Zelfs als de hoek van de gemeenschappelijke normaal verandert, blijft de lengte constant. Deze eigenschap biedt een belangrijk voordeel bij metingen. Het betekent dat zelfs als er enige afwijking is in de positie van het meetgereedschap, dit geen invloed heeft op de uitkomst van de meting.
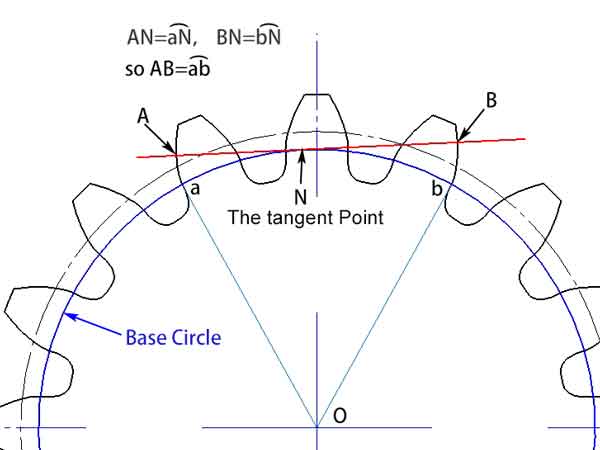
overspannen tandnummer
Het aantal tanden overspannen door de gemeenschappelijke normaallengte van het tandwiel wordt het “aantal overspannen tanden” genoemd en kan worden bepaald aan de hand van de gemeenschappelijke normaal die op de blauwdruk is getekend. Er is een formule om het te berekenen, maar het berekeningsproces kan wat omslachtig zijn, waardoor directe observatie vanaf de bouwtekening eenvoudiger en eenvoudiger is. De formule is
k = zα / 180° + 0,5
Waar:
kis het overspannen tandnummer,zis het aantal tanden,αde drukhoek van het tandwiel op de omtrekcirkel, die in de meeste gevallen 20° isxis de versnelling profielverschuivingscoëfficiënt.
De lengte van de gemeenschappelijke normaal kan ook worden verkregen uit CAD-tekeningen, maar het kan ook worden berekend met een formule. Voor tandwielen met een modificatiecoëfficiënt x = 0 is de formule voor het berekenen van de overspannen tandafstand:
L = m cos α [(k - 0,5)π + z inv α]
Waar:
Lis de lengte van de gemeenschappelijke normaal,αde drukhoek bij de referentiekring,kis het overspannen tandnummer.
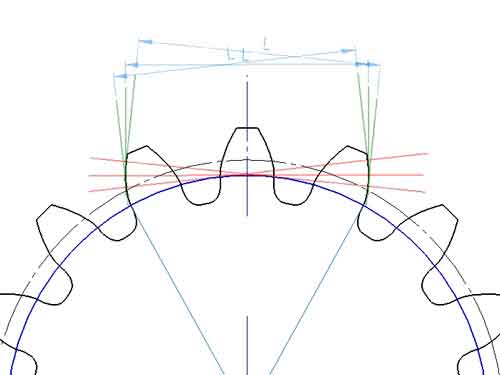
De bovenstaande formules zijn berekend op basis van de modificatiecoëfficiënt x = 0, waarbij de tanddikte aan de steekcirkel s = zm/2, wat de helft van de steek is. Als x > 0, neemt de tanddikte bij de steekcirkel echter toe, wat leidt tot een toename van L, en omgekeerd neemt L af als x < 0. Daarom is het meten van de lengte van de gemeenschappelijke normaal een effectieve methode voor reverse-engineering van tandwielen, waarmee de modificatiecoëfficiënt van het voorbeeldtandwiel kan worden geschat.
Conclusie
Om dit artikel beknopt te houden, zullen we hier niet ingaan op de afleidingen van deze formules, maar ze zullen in andere artikelen aan bod komen.
We hopen dat dit artikel je een duidelijk beeld geeft van het gewone normale. Als je vragen hebt, laat dan hieronder je commentaar achter.