目次
トグル歯車検査方法における共通法線長さの測定
歯車の検査方法について議論する際、共通法線の長さを測定することは、歯車生産およびリバースエンジニアリング検査で広く使用されているシンプルでコスト効率の高い技術を提供します。
この方法は、従来の個々の歯厚測定と比較して、操作を簡素化するだけでなく、点接触による局所的な弾性変形に関連する問題を効果的に回避し、測定精度を向上させます。歯厚用歯車ノギスで歯厚を測定する際には、ノギスが歯面に対して平行を保つことが不可欠であり、これは間違いなく測定の難易度を増加させます。さらに、CNC(コンピュータ数値制御)装置を使用した測定は精密ではありますが、コストが高く、プロセスも煩雑です。.
本記事では、まずインボリュート曲線の基本概念を紹介し、徐々に歯車の共通法線の概念について深く掘り下げていきます。記事の終わりまでに、これを包括的に理解し、この知識を仕事で効果的に応用できるようになるはずです。.
インボリュートの基本概念
インボリュートの紹介:簡略化された理解と基本知識
数学や工学で頻繁に言及されるインボリュートの概念は、簡単な実験を通じて理解できます:非弾性の細い糸が円形の物体(完全な円と考えてください)に巻き付けられていると想像してください。この糸を張ったままゆっくりと解き始めると、糸の端がたどる経路がインボリュートと呼ばれるものを形成します。このプロセスにおいて、円形の物体は「基礎円」と呼ばれ、解かれる糸は「母線」として知られています。“

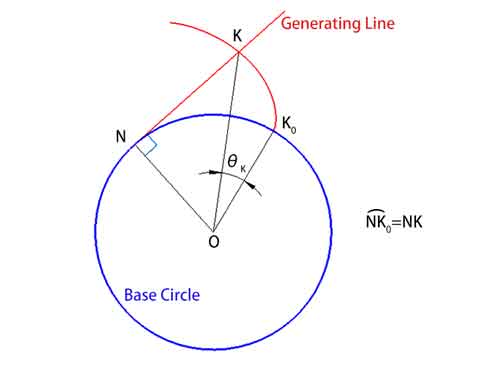
この動作において、母線は基礎円に接線のまま保たれ、インボリュート上の任意の点では、それは曲線に対して垂直です。この角度、すなわち巻き戻し角 θ (∠KOK0)は、インボリュート上の点(K)から基礎円の中心(O)を結ぶ線が、インボリュートの始点(K0)から形成される角度です。.
注目すべきは、糸の長さが変化しないため、基礎円上の弧長(弧 NK0)と母線の長さ(NK)は数値的に等しいことです。.
圧力角αの概念とその可変性
さらに深く掘り下げて、インボリュートに密接に関連する概念である圧力角 αについて議論しましょう。圧力角は、インボリュート上の任意の点における法線(つまり、インボリュートに垂直な線)とその点を通る速度方向との間の角度です。重要な点は、圧力角がインボリュートに沿った各点で変化し、インボリュートの始点ではゼロから始まり、外側に向かって徐々に増加することです。.
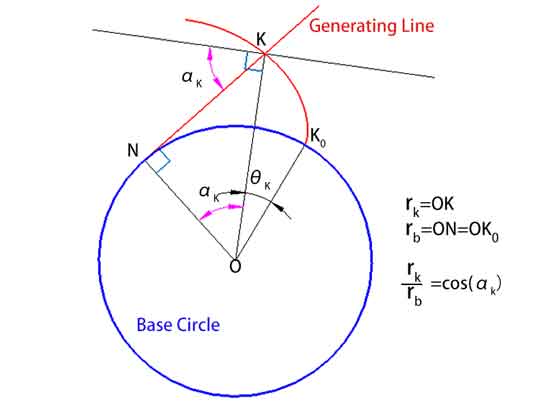
さらに、インボリュート上の点 K から円の中心までの距離 rk は、式 rk = rb / cos(αk) を使用して計算できます。ここで、rb は基礎円の半径、αk は点 K における圧力角です。.
Common Normal Function
巻き戻し角 θ と圧力角 α の間の関数関係は、インボリュート関数と呼ばれ、inv(α) と表記されます。.
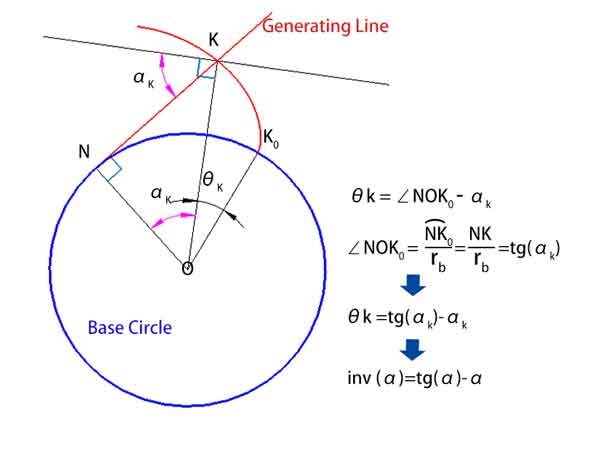
以下の図に示すように、θk = ∠NOK0 - αk
ここで、∠NOK0 は、弧長 NK0 を半径 rb で割った値に等しく、弧長単位で測定され、度に変換することもできます。.
弧長 NK0 = NK であるため、= NK / rb = tg(αk)
したがって、θk = tg(αk) - αkとなります。
つまり、inv(αk) = tg(αk) - αkを意味します。
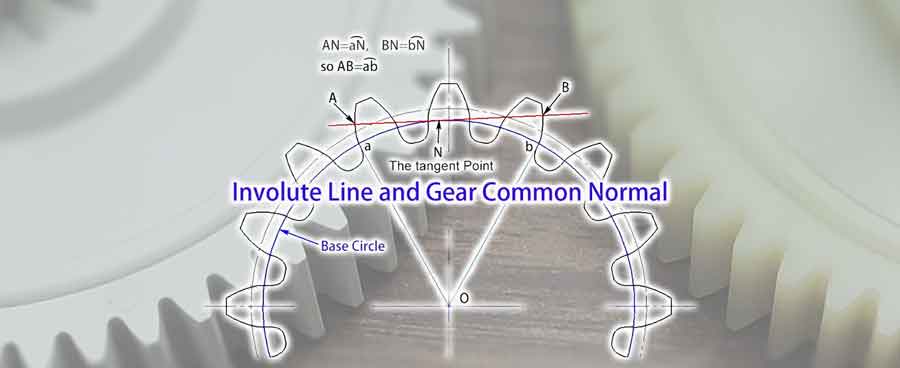
歯車の共通法線の概念
インボリュートの基本概念を理解したところで、次に歯車の共通法線の概念について詳しく見ていきましょう。これは、基礎円上の任意の接線であり、歯車の歯形を数歯分離れた点で交差する線を指します。インボリュートの特性により、この線はこれら2つの歯形を形成するインボリュートに垂直であることがわかります。そのため、共通法線と呼ばれます。.
図から、これら2つの歯形の間に位置する共通法線の長さ(AB)は、基礎円上の弧長abに等しいことが観察できます。共通法線の角度が変化しても、その長さは一定のままです。この特性は、測定において大きな利点を提供します。つまり、測定工具の位置に多少のずれがあったとしても、測定結果には影響しないことを意味します。.
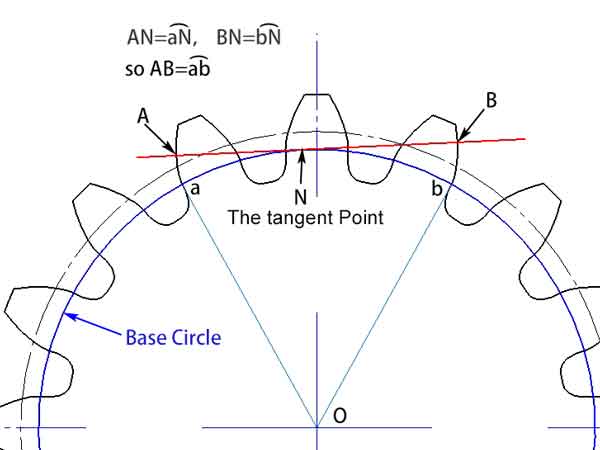
spanned tooth number
歯車の共通法線長さがまたぐ歯数を「またぎ歯数」と呼び、これは図面上に描かれた共通法線から決定できます。計算式はありますが、計算プロセスはやや煩雑なため、図面から直接観察する方がより簡単で直接的です。その計算式は以下の通りです:
k = zα / 180° + 0.5
Where:
kはスパン歯数、,zは歯数、,αこれは円周上の歯車の圧力角であり、ほとんどの場合20°ですxis the gear 歯先修正係数。.
共通法線の長さは、CAD図面からも得ることができますが、公式を用いて計算することも可能です。修正係数x = 0の歯車の場合、スパン歯厚の計算式は以下の通りです:
L = m cos α [(k - 0.5)π + z inv α]
Where:
Lは共通法線の長さ、,αは圧力角、 reference circle,kはスパン歯数。.
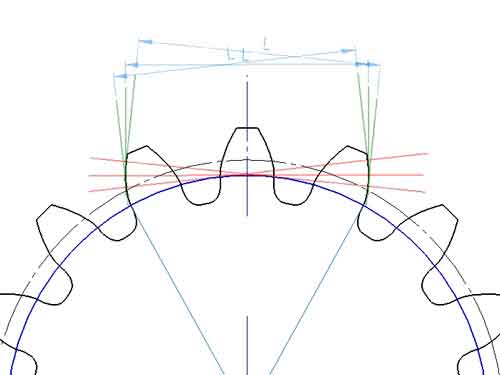
上記の公式は、修正係数x = 0に基づいて計算されています。この場合、ピッチ円上の歯厚はs = zm/2となり、ピッチの半分です。しかし、x > 0の場合、ピッチ円上の歯厚は増加し、それに伴ってLも増加します。逆に、x < 0の場合、Lは減少します。したがって、共通法線の長さを測定することは、歯車のリバースエンジニアリングにおいて有効な方法であり、サンプル歯車の修正係数を推定することが可能です。.
結論
本記事を簡潔にするため、これらの式の導出についてはここでは詳しく説明しませんが、他の記事で取り上げます。.
本記事が共通法線について明確な概念を提供できれば幸いです。ご質問があれば、以下にコメントをお寄せください。.