Table des matières
ToggleMesure de la longueur normale commune dans les méthodes d'inspection des engrenages
Lorsque l'on parle de méthodes d'inspection des engrenages, la mesure de la longueur de la ligne normale commune est une technique simple et rentable largement utilisée dans la production d'engrenages et les inspections d'ingénierie inversée.
Cette méthode, comparée à la mesure traditionnelle de l'épaisseur de chaque dent, non seulement simplifie l'opération, mais évite également les problèmes liés à la déformation élastique locale causée par le contact ponctuel, améliorant ainsi la précision des mesures. Lorsque l'on mesure l'épaisseur d'une dent à l'aide d'un pied à coulisse pour dents de scie, il est essentiel de s'assurer que le pied à coulisse reste parallèle à la surface de la dent, ce qui accroît incontestablement la difficulté de la mesure. De plus, si l'utilisation d'un équipement CNC (Computer Numerical Control) pour la mesure est précise, elle est aussi coûteuse et le processus est lourd.
Cet article commencera par présenter le concept de base de la ligne de développante, en approfondissant progressivement le concept de la normale commune de l'engrenage. À la fin de cet article, vous devriez en avoir une compréhension globale et être en mesure d'appliquer ces connaissances de manière efficace dans votre travail.
Le concept de base de l'involu
Introduction à l'involution : compréhension simplifiée et connaissances de base
La développante, un concept fréquemment mentionné en mathématiques et en ingénierie, peut être comprise par le biais d'une expérience simple : imaginons que nous ayons une corde fine non élastique enroulée autour d'un objet circulaire (imaginez un cercle parfait). Lorsque nous commençons à dérouler lentement cette ficelle tout en la maintenant tendue, la trajectoire que prend l'extrémité de la ficelle forme ce que l'on appelle une involute. Dans ce processus, l'objet circulaire est appelé “cercle de base” et la ficelle qui se déroule est appelée “ligne génératrice”.”

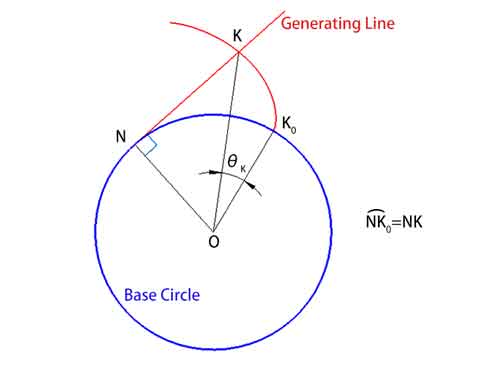
Dans cette action, lagénératrice reste tangente au cercle de base, et en tout point de la développante, elle est perpendiculaire à la courbe. Cet angle, que nous appelons angle de déroulement θ (∠KOK0), est l'angle formé par la droite reliant le point de la développante (K) au centre du cercle de base (O) à partir du point de départ de la développante (K0) .
Il est intéressant de noter que puisque la longueur de la corde ne change pas, la longueur de l'arc sur le cercle de base (arc NK0) et la longueur de la ligne génératrice (NK) sont numériquement égales.
Le concept d'angle de pression α et sa variabilité
Pour aller plus loin, examinons un concept étroitement lié à la développante, à savoir l'angle de pression α. L'angle de pression est l'angle entre la normale en tout point de la développante (c'est-à-dire la ligne perpendiculaire à la développante) et la direction de la vitesse à travers ce point. Il est important de noter que l'angle de pression varie en chaque point de la développante, partant de zéro au début de la développante et augmentant progressivement au fur et à mesure que l'on se déplace vers l'extérieur.
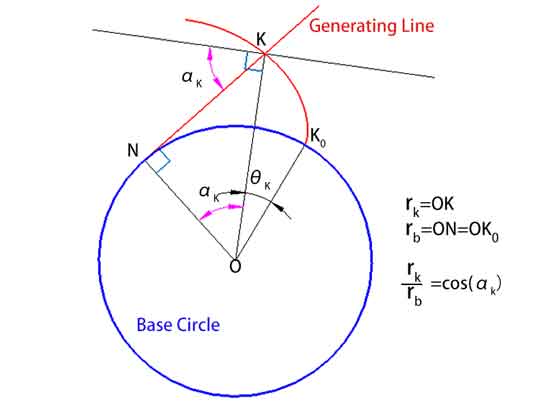
En outre, la distance entre un point K de la développante et le centre du cercle, rk, peut être calculée à l'aide de la formule rk = rb / cos(αk), où rb est le rayon du cercle de base et αk est l'angle de pression au point K.
Fonction normale commune
La relation fonctionnelle entre l'angle de déroulement θ et l'angle de pression α est appelée fonction de développante, désignée par inv(α).
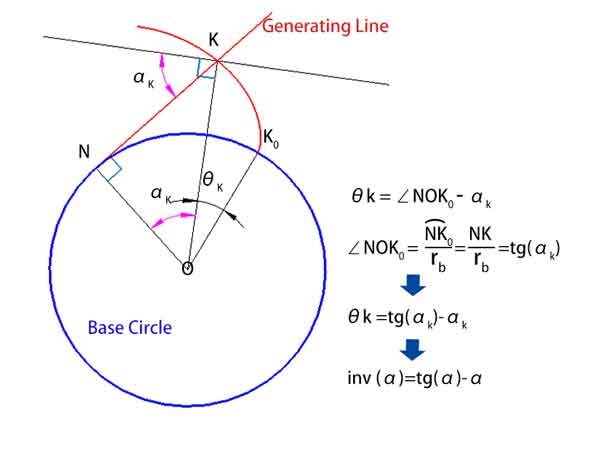
Comme le montre le diagramme ci-dessous, θk = ∠NOK0 - αk
Le ∠NOK0 est égal à lalongueur d'arc NK0 divisée par le rayon rb, mesuré en unités de longueur d'arc, qui peut également être converti en degrés.
Puisque la longueur de l'arc NK0 = NK, alors = NK / rb = tg(αk)
On a donc θk = tg(αk) - αk
Ce qui signifie inv(αk) = tg(αk) - αk
Le concept de la norme commune de l'engrenage
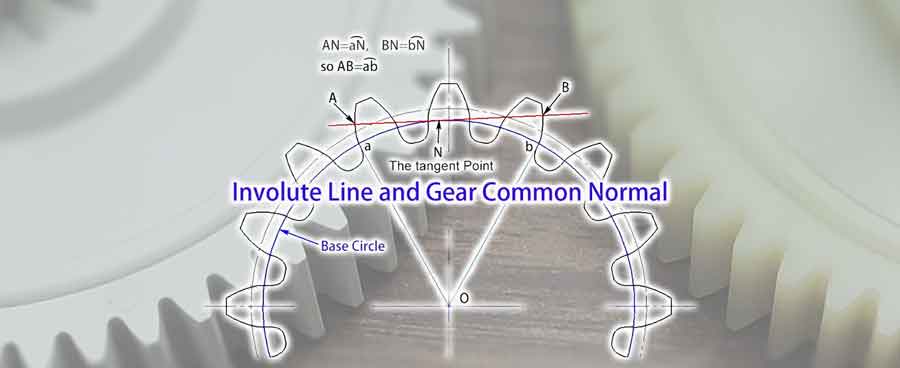
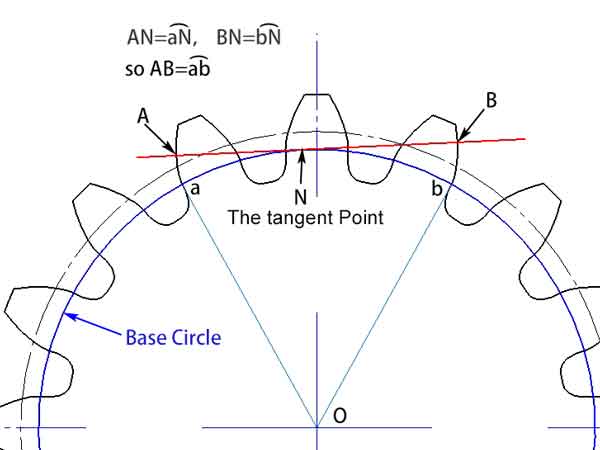
Après avoir compris le concept de base de la développante, nous pouvons maintenant approfondir le concept de la normale commune de l'engrenage. Il s'agit de toute ligne tangente au cercle de base qui intersecte les profils de l'engrenage en des points séparés par plusieurs dents. En raison des caractéristiques de la développante, nous savons que cette ligne est perpendiculaire aux développantes qui forment ces deux profils d'engrenage, c'est pourquoi on l'appelle la normale commune.
Sur les illustrations, on constate que la llongueur de la normale commune (AB), nichée entre ces deux profils d'engrenage, est égale à la longueur de l'arcab sur le cercle de base. Même si l'angle de la normale commune change, sa longueur reste constante. Cette caractéristique offre un avantage significatif en matière de mesures. Cela signifie que même s'il y a un écart dans la position de l'outil de mesure, cela n'affectera pas le résultat de la mesure.
nombre de dents enjambées
Le nombre de dents couvertes par la longueur normale commune de l'engrenage est appelé “nombre de dents couvertes”, qui peut être déterminé à partir de la normale commune dessinée sur le plan. Il existe une formule pour le calculer, mais le processus de calcul peut être quelque peu fastidieux, ce qui rend l'observation directe à partir du plan plus simple et plus directe. La formule est la suivante :
k = zα / 180° + 0,5
Où ?
kest le numéro de la dent étendue,zest le nombre de dents,αest l'angle de pression de l'engrenage sur le cercle de circonférence, qui est de 20° dans la plupart des casxest l'engrenage coefficient de décalage du profil.
La longueur de la normale commune peut également être obtenue à partir de dessins CAO, mais elle peut aussi être calculée à l'aide d'une formule. Pour les engrenages dont le coefficient de modification x = 0, la formule de calcul de la distance entre les dents est la suivante :
L = m cos α [(k - 0.5)π + z inv α]
Où ?
Lest la longueur de la normale commune,αest l'angle de pression au niveau du cercle de référence,kest le numéro de la dent étendue.
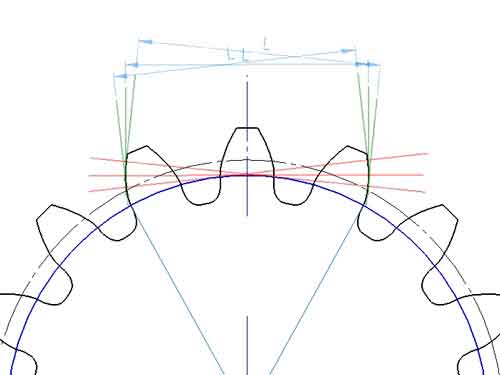
Les formules mentionnées ci-dessus sont calculées sur la base du coefficient de modification x = 0, où l'épaisseur de la dent au cercle primitif s = zm/2, qui est la moitié du pas. Toutefois, si x > 0, l'épaisseur de la dent au niveau du cercle primitif augmente, ce qui entraîne une augmentation de L, et inversement, L diminue si x < 0. Par conséquent, la mesure de la longueur de la normale commune est une méthode efficace pour la rétro-ingénierie des engrenages, permettant d'estimer le coefficient de modification de l'échantillon d'engrenage.
Conclusion
Dans un souci de concision, nous n'entrerons pas ici dans la dérivation de ces formules, qui seront abordées dans d'autres articles.
Nous espérons que cet article vous donnera une idée claire de la norme commune. Si vous avez des questions, n'hésitez pas à laisser vos commentaires ci-dessous.