Inhoudsopgave
SchakelDit is een eenvoudigere versie van tandwielterminologie en formules voor tandberekening.
Deze post is bedoeld om de tandwielterminologie en tandberekeningsformules op een eenvoudigere manier uit te leggen voor beginners, en ook voor degenen die lang geleden tandwielen hebben geleerd maar het snel weer willen oppakken.
De tandwielen hebben veel parameters die wat wiskunde en geometrische kennis vereisen om ze volledig te begrijpen. U hoeft echter niet te diep in te gaan op de basisconcepten van tandwielkennis; na het lezen van dit bericht zou u in staat moeten zijn om voorlopige tandwielontwerpen te maken of effectief te communiceren met tandwielontwerpers.
Laten we beginnen met de basisvorm van tandwielen, de rechte tandwielen:
Inhoudsopgave
1. Aantal tanden (z); 2. Referentiecirkel en referentiediameter (d); 3. Module (m); 4. Hartafstand (a); 5. Drukhoek (α); 6. Minimum aantal tanden (zmin); 7. Profielverschuivingscoëfficiënt (x); 8. Samenvattende tabel.
1. Tandenaantal (z)
Dit is vrij eenvoudig, het is het aantal tanden van het tandwiel.
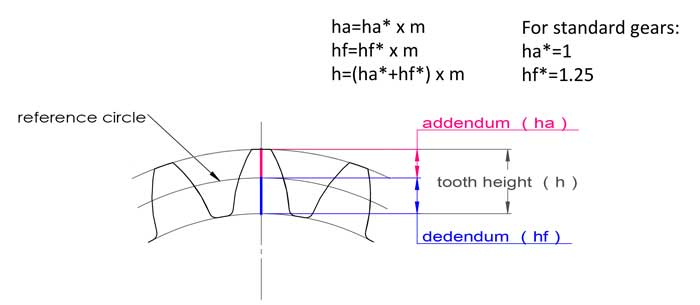
2. Steekcirkel en steekcirkeldiameter (d)
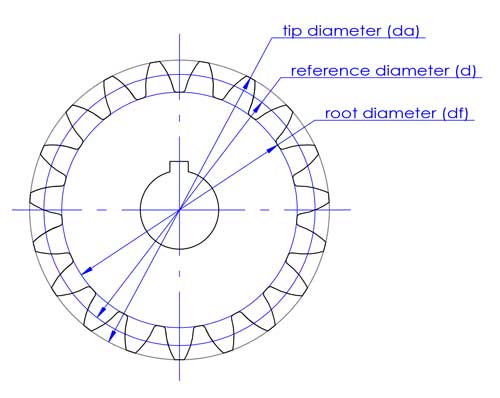
De topdiameter (da) en voetdiameter (df) komen overeen met de boven- en onderkant van de tanden.
De referentiediameter wordt gebruikt bij het ontwerpen en berekenen van tandwielen. Het heeft directe verbanden met andere belangrijke tandwielparameters zoals de module (m), de asafstand (c) en de drukhoek (α).
De topdiameter (da) en voetdiameter (df) komen overeen met de boven- en onderkant van de tanden.
De referentiediameter wordt gebruikt bij het ontwerpen en berekenen van tandwielen. Het heeft directe verbanden met andere belangrijke tandwielparameters zoals de module (m), de asafstand (c) en de drukhoek (α).
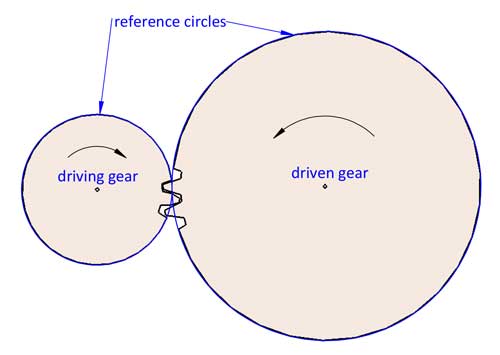
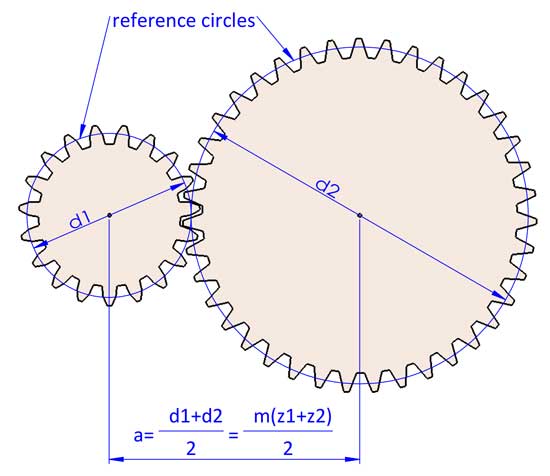
Het draaien van 2 tandwielen kan worden beschouwd als het ingrijpend draaien van 2 referentiecirkels zonder slip. De overbrengingsverhouding i=d2/d1. d1 en d2 verwijzen naar de referentiediameters van 2 in elkaar grijpende tandwielen (tandwiel 1 is het aandrijftandwiel, en tandwiel 2 is het aangedreven tandwiel).

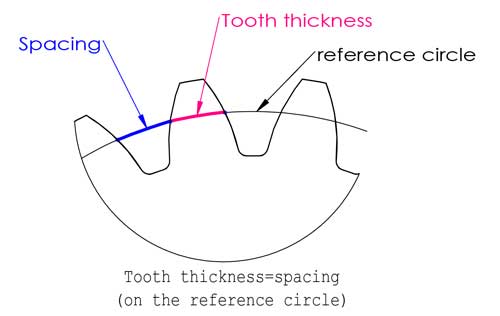
De referentiecirkel bevindt zich ergens tussen de top en de voet van de tanden, meestal is het waar de tanddikte gelijk is aan de tussenruimte, maar dit is niet altijd het geval (we zullen later in deze post over profielverschuiving praten).
3. Module (m)
De module is waarschijnlijk de belangrijkste tandwielparameter, en het komt bijna overal voor in tandberekeningsformules. Eigenlijk is het niet zo moeilijk te begrijpen als je misschien denkt. Laten we eerst begrijpen wat de steek is, Steek is de booglengte tussen overeenkomstige punten op aangrenzende tanden, meestal op de referentiecirkel.
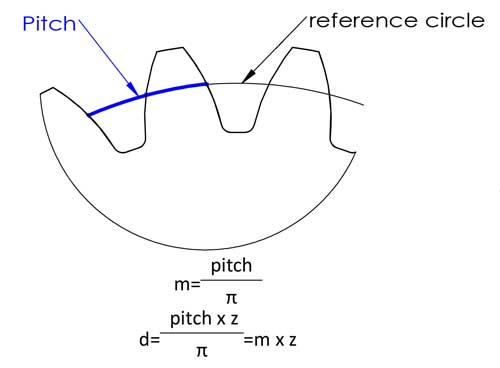

Dan hebben we de referentiediameter d=omtrek/π=steek*z/π. Om de berekening eenvoudiger te maken, definiëren we de steek/π als de module, en nu hebben we de vergelijking d=m*z. Dit maakt de berekening een stuk eenvoudiger, toch? De modules zijn gestandaardiseerd in de volgende getallen (eenheid: mm):
Eerste reeks (aanbevolen): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Tweede reeks (minder gebruikt): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Voor spuitgegoten kunststof tandwielen is het echter niet nodig om deze standaard modulen te gebruiken, aangezien de tanden niet worden gesneden met standaard tandfreesmachines.
Nu hebben we de overbrengingsverhouding i=d2/d1=z2/z1 (tandwiel 1 is het aandrijftandwiel, en tandwiel 2 is het aangedreven tandwiel).
De module heeft ook te maken met de tandhoogte, voor standaard tandwielen is de tandhoogte gelijk aan 2,25*m:
kophoogte ha=1*m, voethoogte hf=1,25*m, tandhoogte h=2,25*m.
4. Hartafstand (a)
2 ingrijpende tandwielen hebben altijd dezelfde module, anders passen ze niet. Nu kunnen we concluderen dat a=(d1+d2)/2=m(z1+z2)/2, maar dit kan iets anders zijn bij het aanbrengen van aanpassingen aan de tandwielgeometrieën (profielverschuiving).
Eenvoudig gezegd, zoals de naam al aangeeft, is het de hoek tussen de richting van de contactkracht op het contactpunt van de tand en de bewegingsrichting van dat punt op het tandprofiel.
In de geometrie is het de hoek tussen de lijn loodrecht op het evolvente tandprofiel en de lijn loodrecht op zijn radiale lijn.
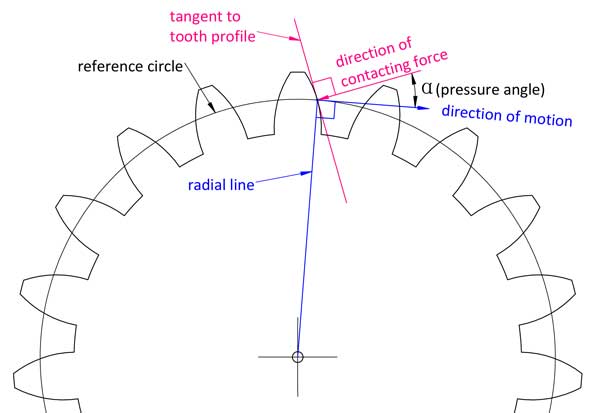
Als u de drukhoek volledig wilt begrijpen, moet u dieper ingaan op het begrijpen van de involuutlijn van het tandprofiel. Dit is slechts een eenvoudigere manier van uitleg.
Verschillende punten op het tandprofiel hebben verschillende drukhoeken, maar wanneer we het hebben over de drukhoek van een tandwiel, verwijst dit meestal naar die op de referentiecirkel. De meeste tandwielen gebruiken 20° als drukhoek, sommige zijn 14,5° of 25°. 2 in elkaar grijpende tandwielen moeten dezelfde module en drukhoek hebben.
6. Minimum tandenaantal (zmin) zonder ondertanding in tandwiel
Je kunt niet zomaar elk gewenst aantal tanden van het tandwiel hebben. Als er te weinig tanden zijn, zal de voet van de tanden onder het grenspunt liggen, met als gevolg dat wanneer de tanden worden gemaakt door tandfreesmachines, een overmatig deel van de tandwortel wordt weggesneden.
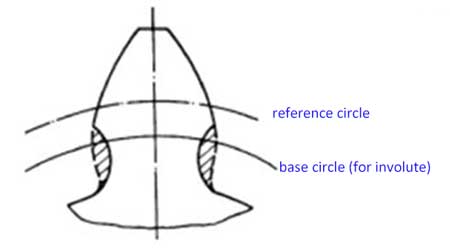
7. Profielverschuivingscoëfficiënt (x)
Meestal voor het tandprofiel is de tandkop ha=1*m, en de tandvoet hf=1,25*m, maar het tandprofiel kan een beetje omhoog of omlaag worden verschoven:
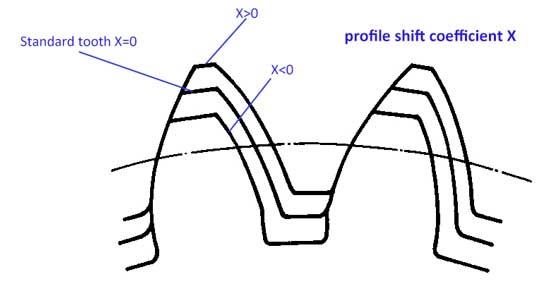

Nu hebben we de profielverschuivingscoëfficiënt (x). Wanneer het profiel naar boven wordt verschoven, is de waarde van x positief (x>0), en als het profiel naar beneden wordt verschoven, is de waarde van x negatief (x<0).
Met de verschuiving van het tandprofiel hebben we nu:
- kophoogte ha=(1+x)*m
- voethoogte hf=(1.25-x)*m
Tandhoogte h=ha+hf=2,25*m, het is nog steeds hetzelfde als standaard tanden.
De belangrijkste redenen voor profielverschuiving zijn:
1) Met profielverschuiving kunnen we ondertanden vermijden met minder tanden. De formule is als volgt:
xmin=(17-z)/17
Bijvoorbeeld, als je het aantal tanden op 14 wilt hebben, dan X=(17-14)/17=0,176
2) Fijnafstelling van de hartafstand
a=[(m+x1)z1+(m+x2)z2]/2, dus de hartafstand hoeft niet (z1+z2)*m te zijn.
3) Maak het rondsel sterker. Meestal faalt het rondsel eerder dan het tandwiel, door een positieve profielverschuiving toe te voegen, wordt de voet van het rondsel breder (terwijl de top smaller wordt) waardoor het sterker wordt.
Samengevat:
| # | Item | Symbool | Formule |
|---|---|---|---|
| 1 | tandenaantal | z | |
| 2 | module | m | m=steek/π |
| 3 | overbrengingsverhouding | i | i=d2/d1=z2/z1 1: aandrijftandwiel, en 2: aangedreven tandwiel |
| 4 | kopcoëfficiënt | da* | da*=1+x x=0 voor standaardtandwielen |
| 5 | voetcoëfficiënt | df* | df*=1.25-x |
| 6 | profielverschuivingscoëfficiënt | x | Voor standaardtandwielen, x=0 |
| 7 | drukhoek | α | α=20° voor de meeste tandwielen Andere minder gebruikte zijn 14,5° en 25°. |
| 8 | referentiediameter | d | d=mz |
| 9 | topdiameter | da | da=d+2Ha* x m, da=(z+2ha*) m Voor standaardtandwielen, da=(z+2) x m |
| 10 | voetdiameter | df | df=d-2Hf* x m, df=(z-2hf*) x m Voor standaardtandwielen, df=(z-2,5) x m |
| 11 | kophoogte | ha | ha=m x ha* Voor standaardtandwielen, ha=m |
| 12 | voethoogte | hf | hf=m x hf* Voor standaardtandwielen, hf=1,25m |
| 13 | tandhoogte | h | h=m x (ha*+hf*) ha*+Hf*=2,25 voor de meeste tandwielen |
| 14 | hartafstand | a | a=m x (z1+z2)/2 voor standaardtandwielen a=[(m+x1)z1+(m+x2)z2]/2 voor profielverschoven tandwielen |
| 15 | Minimum aantal tanden zonder ondertanding | Zmin | Zmin=2ha*/sinα^2 Zmin=17 wanneer ha*=1, α=20° |
| 16 | Minimale profielverschuiving zonder ondertanding | Xmin | Xmin=(17-z)/17 |
Veelgestelde vragen
Inleiding tot tandwielkrachten
Tijdens het ingrijpproces tussen twee tandwielen kan de kracht die door het aandrijftandwiel op het aangedreven tandwiel wordt uitgeoefend, worden ontbonden in een normaalkracht loodrecht op het oppervlak van het aangedreven tandwiel en een tangentiële kracht loodrecht op de normaalkracht. De tangentiële kracht neemt niet deel aan het aandrijven van het aangedreven tandwiel en veroorzaakt slijtage tussen de twee tandwielen. De hoek op het ingrijppunt van de aandrijvende en aangedreven tandwielen is het grootst aan het begin en einde van de ingreep en kleiner in het midden. Wanneer het ingrijppunt zich op de middellijn van de twee tandwielen bevindt, is deze gelijk aan nul. Daarom kan een kleinere hoek de overbrengingsefficiëntie verbeteren en slijtage verminderen.
Relatie tussen drukhoek en ingrijphoek
De drukhoek is direct gerelateerd aan de ingrijphoek. Aan de andere kant resulteert een kleinere drukhoek in dunnere tandwortels, wat de sterkte van de tandwielen vermindert. Daarom is het belangrijk om een balans te vinden.
Industriële normen voor tandwieldrukhoeken
- In de huidige industriële productie gebruiken de meeste standaard tandwielen een drukhoek van 20°.
- Tandwielen ontworpen voor lichte belastingen en hoge snelheden gebruiken vaak een drukhoek van 14,5°, wat de voordelen heeft van minder geluid en hogere overbrengingsefficiëntie.
- Tandwielen ontworpen voor lage snelheid en zware belasting gebruiken een drukhoek van 25°, wat een hogere tandsterkte biedt, maar ten koste van lagere overbrengingsefficiëntie en meer geluid.
Kunststoftandwielen
Voor kunststof tandwielen kan elke drukhoek worden gekozen, aangezien standaard snijgereedschappen niet vereist zijn voor hun fabricage. Voor eenvoud in het ontwerp is het echter gebruikelijk om deze standaardwaarden aan te houden.
De omtrekcirkel is de basis voor tandwielberekeningen. De diameter ervan wordt berekend als de module (m) vermenigvuldigd met het aantal tanden (Z). In wezen is het een theoretische cirkel die voornamelijk wordt gebruikt voor berekeningen, waarbij andere tandwielparameters ervan zijn afgeleid.
De steekcirkel daarentegen wordt gedefinieerd tijdens de daadwerkelijke ingreep van twee tandwielen. Het is de cirkel gevormd door het snijpunt van de gemeenschappelijke normaal van de tandwielen en de lijn die hun middelpunten verbindt, die door het raakpunt gaat. De steekcirkels van twee ingrijpende tandwielen raken elkaar. De omtrekcirkels zijn echter niet altijd raak.
In standaard tandwielontwerpen overlappen de omtrekcirkel en de steekcirkel doorgaans. Als de hartafstand echter wordt aangepast om de speling te vergroten of als de tandwielen zijn aangepast, kunnen de omtrekcirkel en de steekcirkel verschillen.
Ja. In standaardontwerpen zijn de tanddikte en de spleetbreedte op de omtrekcirkel gelijk.
In praktische toepassingen wordt de tanddikte echter iets dunner gemaakt om wat speling mogelijk te maken terwijl de standaard hartafstand behouden blijft.
Een methode is om de tanddikte iets kleiner te maken dan de spleetbreedte op de omtrekcirkel.
Een andere methode is om de tandwielen te installeren op een hartafstand die iets groter is dan de standaard.
De vereiste grootte van de speling hangt af van de fabricagenauwkeurigheid van de tandwielen; hogere precisie vermindert de behoefte aan speling.
De grondcirkel van een tandwiel is de cirkel waaruit zijn evolvente wordt gegenereerd. De steek ervan is de booglengte tussen identieke punten op de profielen van twee aangrenzende tanden op de grondcirkel, dus:
Pb = Db/Z.
Hier is Db de diameter van de grondcirkel.
Of Pb = Df * cos(α) / Z = mπ * cos(α),
waarbij Df de diameter van de omtrekcirkel is, m de module van het tandwiel en α de drukhoek van de omtrekcirkel.
1. Voor rechte tandwielen is het vereist dat de ingreep van één paar tanden gesynchroniseerd is met de ingreep van het vorige paar. Dit vereist dat hun grondcirkelsteken gelijk zijn, wat betekent:
m1 * cos(α1) = m2 * cos(α2).
Hieruit kan worden afgeleid dat de modules (m) van een paar ingrijpende tandwielen niet noodzakelijk gelijk hoeven te zijn.
2. Tegelijkertijd is de mate van ingreep (contactverhouding ε) groter dan 1.
Voor tandwielen vervaardigd met standaard snijgereedschappen, vanwege de standaardisatie en serialisatie van de gereedschappen, is het gebruikelijk om dezelfde module en drukhoek van de omtrekcirkel voor beide tandwielen te gebruiken.
3. Voor schuine tandwielen is het ook noodzakelijk dat hun schuine hoeken gelijk zijn, ervan uitgaande dat hun installatie-assen parallel zijn.
De contactverhouding (ε) is de lengte van het gemeenschappelijke normaalsegment tussen twee ingrijpende tandwielen, dat wordt gesneden door de kopcirkels van de tandwielen, gedeeld door de grondsteek (Pb) van het tandwiel.
- Wanneer ε <1, kunnen de tandwielen niet correct functioneren omdat er momenten zijn waarop geen tanden in contact zijn.
- Als 1 < ε < 2, zijn er momenten waarop slechts één tand in contact is. Bijvoorbeeld, met ε = 1,63 kun je je voorstellen dat gemiddeld 1,63 paar tanden ingrijpen. Tijdens 37% van het overbrengingsproces is slechts één tand in ingrijping, terwijl tijdens 63% twee tanden in ingrijping zijn, wat leidt tot een grotere impact tijdens de overbrenging.
- Als ε > 2, zijn op elk moment meer dan twee paar tanden in contact, wat resulteert in een soepelere overbrenging.
Het aantal tanden (Z) op de tandwielen is een belangrijke factor die de contactverhouding beïnvloedt.
Voor kleinere tandwielen worden vaak schuine tandwielen gebruikt om de contactverhouding te vergroten. De fabricagekosten van schuine tandwielen zijn echter aanzienlijk hoger dan die van rechte tandwielen.
Een andere methode is het gebruik van een kleinere drukhoek van de steekcirkel, maar dit heeft een beperkt effect.
De levensduur van een tandwiel wordt voornamelijk bepaald door slijtage en vermoeidheidsbreuk. Deze problemen ontstaan door verschillende factoren zoals lage tandwielprecisie, ongeschikte speling, slechte smering, oververhitting en meer. Hoewel het lastig is om de levensduur met empirische formules te berekenen, zijn de precisie van het tandwiel en het gebruikte materiaal cruciale factoren voor de levensduur.



Reacties zijn gesloten.