This is a simpler version of gear terminology and teeth calculation formulas
This post is to explain the gear terminologies and teeth calculation formulas in an easier way for beginners, and also for those who have learned gears long ago but want to pick up again quickly.
The gears have many parameters that will take a bit of mathematics and geometrical training to fully understand them. However, You do not need to go too deep into the basic concepts of gear knowledge, after you have read this post, you should be able to make preliminary gear designs or have an effective communication with gear designers.
Let’s get started from the basic gear form, the spur gears:
Table of content
1. Teeth number (z); 2. Reference circle and reference diameter (d); 3. Module (m); 4. Center distance (a); 5. Pressure angle (α); 6. Minimum teeth number (zmin); 7. Profile shift coefficient (x); 8. Summary table.
1. Teeth number (z)
This is pretty straightforward, it is the number of teeth of the gear.
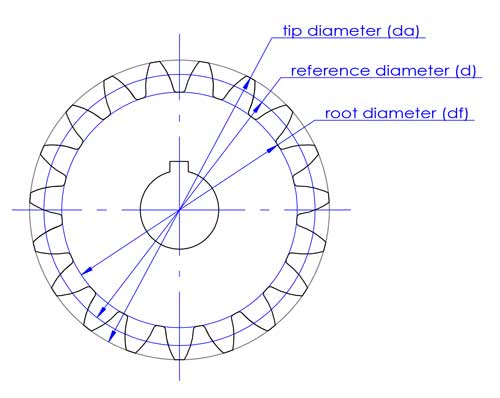
2. Reference circle and reference diameter (d)
The tip diameter (da) and root diameter (df) correspond to the top and bottom of the teeth.
The reference diameter is used in gear designing and calculation. It has direct connections with other important gear parameters like the module (m), center distance (c) and pressure angle (α).
The tip diameter (da) and root diameter (df) correspond to the top and bottom of the teeth.
The reference diameter is used in gear designing and calculation. It has direct connections with other important gear parameters like the module (m), center distance (c) and pressure angle (α).
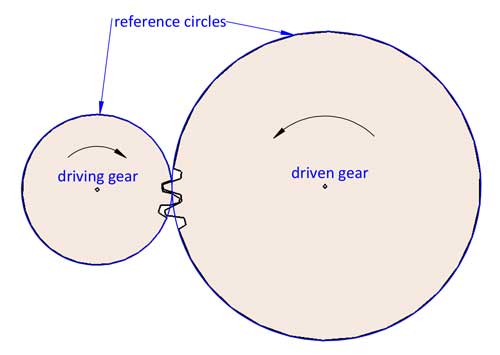
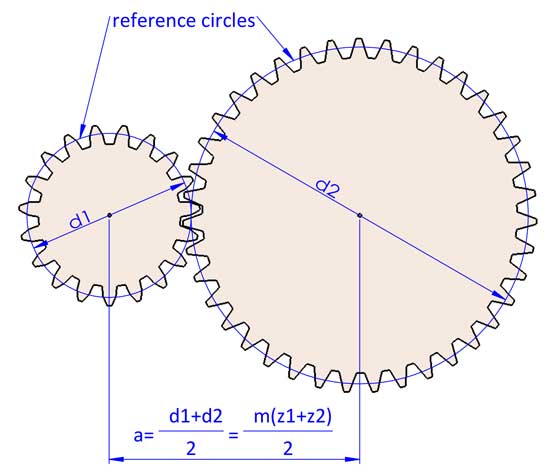
The turning of 2 gears can be considered engaged turning of 2 reference circles without slippage. The gear ratio i=d2/d1. d1 and d2 refer to the reference diameters of 2 mating gears (gear 1 is the driving gear, and gear 2 is the driven gear).
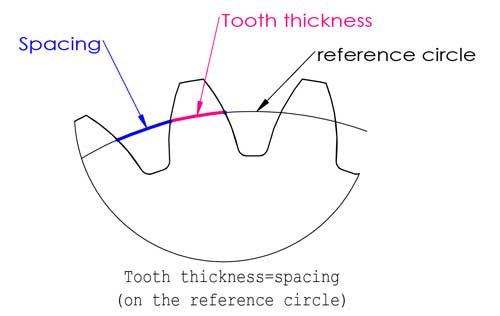
The reference circle is located somewhere between the tip and bottom of the teeth, usually it is where the tooth thickness equals to the spacing, but this is not always the case (we will talk about profile shifting later in this post).
3. Module (m)
The module is probably the most important gear parameter, and it appears almost everywhere in teeth calculation formulas. Actually, it is not so difficult to understand as you might imagine. First let’s understand what the pitch is, Pitch is the arc length between corresponding points on adjacent teeth, usually on the reference circle.
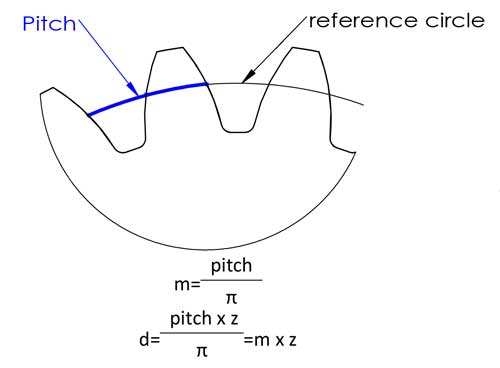
Then we have the reference diameter d=circumference/π=pitch*z/π, to make the calculation easier, we define the pitch/π as the module, and now we have the equation of d=m*z, this makes the calculation a lot easier, right? The modules have been standardized in the following numbers （unit: mm）:
First series (recommeded): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Second series (less used): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
However, for injection-molded plastic gears, there is no need to adopt these standard module numbers, since the teeth are not cut by standard tooth cutters.
Now we have the gear ratio i=d2/d1=z2/z1 (gear 1 is the driving gear, and gear 2 is the driven gear).
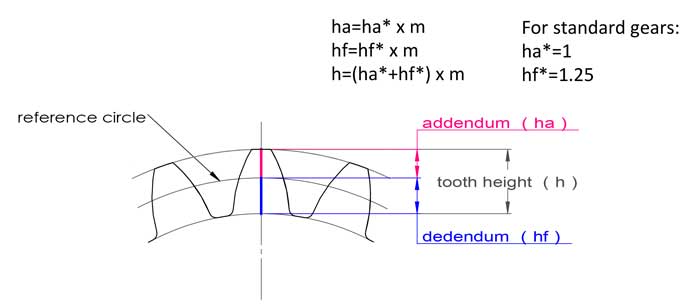
The module also has to do with the tooth height, for standard gears, the tooth height equals to 2.25*m:
addendum ha=1*m, dedendum hf=1.25*m, tooth height h=2.25*m.
4. Center distance (a)
2 meshing gears always have the same module otherwise they don’t match. Now we can come to the conclusion that a=(d1+d2)/2=m(z1+z2)/2, but it can be slightly different while making some adjustments on the gear geometries (tooth profile shifting).
5. Pressure angle (α)
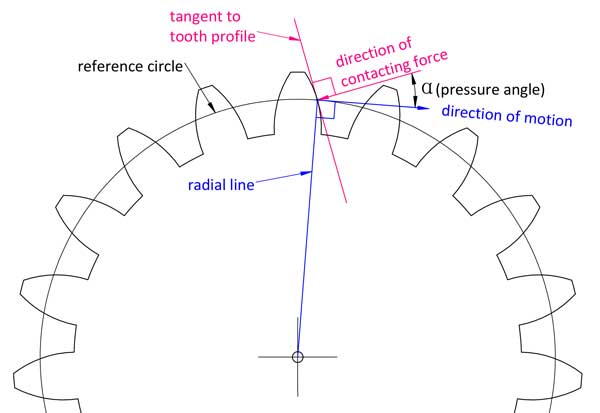
Simply put, as its name suggests, it is the angle between the direction of contacting force on the contact point of the tooth and direction of motion of that point on the tooth profile.
In geometry, it is the angle between the line normal to the involute tooth profile and the line normal to its radial line.
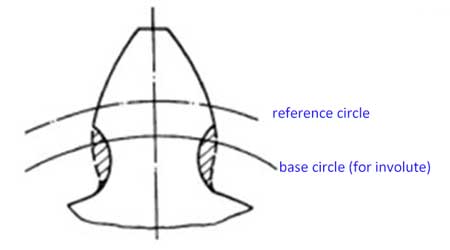
If you want to fully understand the pressure angle then you need to go deeper to understand the involute line of the tooth profile. This is just an easier way of explanation.
Different points on the tooth profile have different pressure angles, but when we talk about the pressure angle of a gear, it usually refers to that on the reference circle. Most gear use 20°as the pressure angle, some are 14.5°or 25°. 2 mating gears must have the same module and pressure angle.
6. Minimum teeth number (zmin) without undercutting in gear
You can not have any teeth number of the gear as you want. If there are too few teeth, the bottom of the teeth will be below the limit point, as a consequence, when the teeth are made by tooth cutters, an excess part of the teeth root will be cut off.
7. Profile shift coefficient (x)
Usually for the tooth profile, the teeth addendum ha=1*m, and the dedendum hf=1.25*m, however the teeth profile can be moved up or down a little bit:
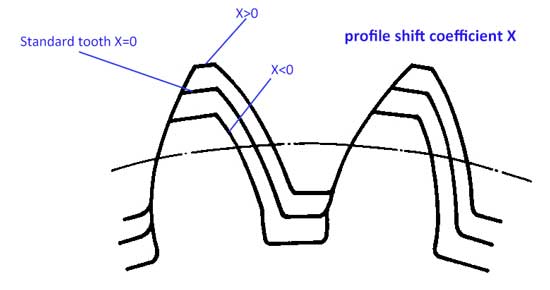
Now we have the profile shift coefficient (x). When the profile is moved upwards, the value of x is positive (x>0), and if the profile is moved downwards, the value of x is negative (x<0).
With the movement of teeth profile, now we have:
- addendum ha=(1+x)*m
- dedendum hf=(1.25-x)*m
Tooth height h=ha+hf=2.25*m, it is still the same as standard teeth.
Main reasons for profile shift are:
1) With profile shifted, we can avoid teeth undercutting with fewer teeth number. The formula is as follows:
xmin=(17-z)/17
For example, if you want to the teeth number to be 14, then X=(17-14)/17=0.176
2)Fine tune of center distance
a=[(m+x1)z1+(m+x2)z2]/2, so the center distance does not have to be (z1+z2)*m
3)Make the pinion stronger. Usually, the pinion fails prior to the gear, by adding a positive profile shift, the bottom the pinion becomes wider (while the tip becomes narrower) thus making it stronger.
In summary:
| # | Item | Symbol | Formula |
|---|---|---|---|
| 1 | teeth number | z | |
| 2 | module | m | m=pitch/π |
| 3 | gear ratio | i | i=d2/d1=z2/z1 1: driving gear, and 2: driven gear |
| 4 | addendum coefficient | da* | da*=1+x x=0 for standard gears |
| 5 | dedendum coefficient | df* | df*=1.25-x |
| 6 | profile shift coefficient | x | For standard gears,, x=0 |
| 7 | pressure angle | α | α=20° for most gears Other less used are 14.5° and 25°. |
| 8 | referernce diameter | d | d=mz |
| 9 | tip diameter | da | da=d+2Ha* x m, da=(z+2ha*) m For standard gears, da=(z+2) x m |
| 10 | root diameter | df | df=d-2Hf* x m, df=(z-2hf*) x m For standard gears, df=(z-2.5) x m |
| 11 | addendum | ha | ha=m x ha* For standard gears, ha=m |
| 12 | dedendum | hf | hf=m x hf* For standard gears, hf=1.25m |
| 13 | tooth height | h | h=m x (ha*+hf*) ha*+Hf*=2.25 for most gears |
| 14 | center distance | a | a=m x (z1+z2) for standard gears a=[(m+x1)z1+(m+x2)z2]/2 for profile shifted gears |
| 15 | Mininum teeth number without undercutting | Zmin | Zmin=2ha*/sinα^2 Zmin=17 when ha*=1, α=20° |
| 16 | Minimun profile shift without undercutting | Xmin | Xmin=(17-z)/17 |
Related posts
How to work with your plastic manufacturer on plastic gears
thank you very much
Thank You!
it’s very helpful
comprehensive explan. thanks
I believe there is a typo in #4…
(d1+d2)/z = m(z1+z2)/2 should be (d1+d2)/2 =m (z1+z2)/2
Thank you for pointing out this error, I have corrected it.
For Zmin; do you divide by sine squared alpha? Or sine 2alpha?
I believe it is written both ways. One in the section and one in the summary.
It means the square of sinα. I have updated on the post so you can take a look, since it does not allow me to use superscripts (on the number 2) in the comment, I think it is easier to update the post content. I also noticed on the table, I wrote it as sin2α, this is also because limitation of using superscripts in the table, it can cause a little confusion, so I have changed it to sinα^2. Thank you for pointing that out.