目次
トグルこれは、歯車用語と歯数計算式の簡易版です。
この投稿は、歯車の専門用語と歯数計算式を、初心者や以前に学んだが再び素早く復習したい方々のために、より分かりやすく説明するものです。.
歯車には多くのパラメータがあり、それらを完全に理解するには多少の数学的および幾何学的知識が必要です。しかし、歯車の基本的な概念について深く掘り下げる必要はありません。この投稿を読んだ後、歯車の予備的な設計ができるようになるか、歯車設計者と効果的にコミュニケーションを取れるようになるはずです。.
基本的な歯車形状である平歯車から始めましょう:
目次
1. 歯数 (z)
これは非常に単純で、歯車の歯数を指します。.
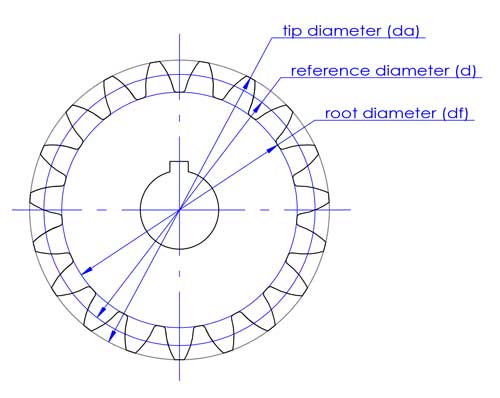
2. 基準円と基準直径 (d)
先端直径(da)と歯元直径(df)は、歯の頂部と底部に対応します。.
基準円直径は、歯車の設計や計算に使用されます。これはモジュール(m)、中心距離(c)、圧力角(α)などの他の重要な歯車パラメータと直接関連しています。.
先端直径(da)と歯元直径(df)は、歯の頂部と底部に対応します。.
基準円直径は、歯車の設計や計算に使用されます。これはモジュール(m)、中心距離(c)、圧力角(α)などの他の重要な歯車パラメータと直接関連しています。.
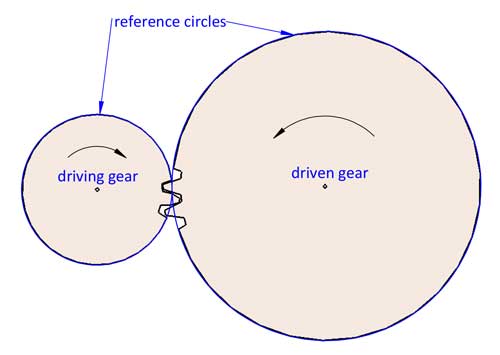
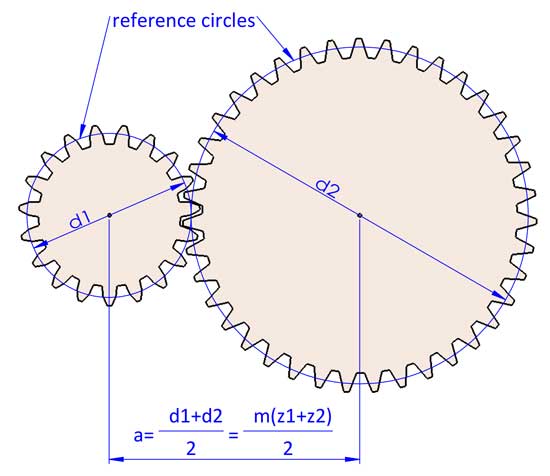
2つの歯車の回転は、滑りなしで2つの基準円が噛み合って回転すると考えることができます。歯車比 i=d2/d1 です。d1 と d2 は、2つの噛み合う歯車の基準円直径を指します(歯車1は駆動歯車、歯車2は従動歯車です)。.

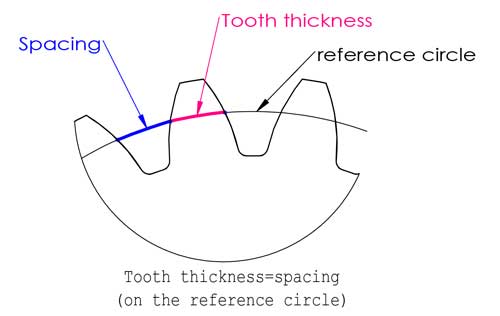
基準円は、歯の先端と底部の間に位置し、通常は歯厚が歯間隔と等しくなる場所ですが、常にそうとは限りません(この投稿の後半でプロファイルシフトについて説明します)。.
3. モジュール (m)
モジュールはおそらく最も重要な歯車パラメータであり、歯数計算式のほぼすべての場所に現れます。実際、想像するほど理解するのは難しくありません。まず、ピッチが何かを理解しましょう。ピッチは、通常基準円上で、隣接する歯の対応する点間の円弧長さです。.
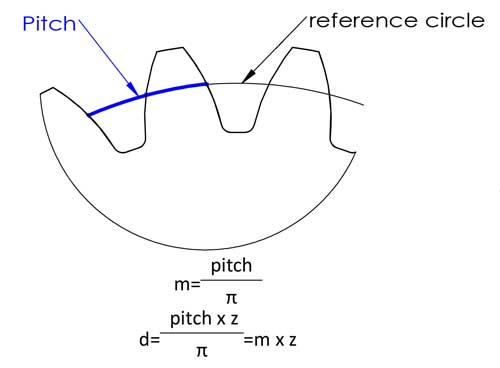

次に、基準直径 d=円周/π=ピッチ*z/π があります。計算を簡単にするために、ピッチ/π をモジュールと定義し、d=m*z という式が得られます。これで計算がずっと簡単になりますね?モジュールは以下の数値に標準化されています(単位:mm):
第一系列(推奨):0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
第二系列(使用頻度低):0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
ただし、射出成形プラスチック歯車の場合、歯は標準的な歯切り工具で切削されないため、これらの標準モジュール番号を採用する必要はありません。.
ここで、歯車比 i=d2/d1=z2/z1 となります(歯車1は駆動歯車、歯車2は従動歯車です)。.
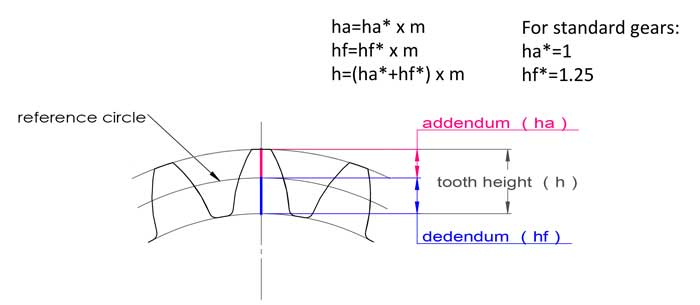
モジュールは歯高とも関係しており、標準歯車の場合、歯高は 2.25*m に等しくなります:
歯先高さ ha=1*m、歯元高さ hf=1.25*m、歯の高さ h=2.25*m。.
4. 中心距離 (a)
2つの噛み合う歯車は常に同じモジュールを持ちます。そうでなければ噛み合いません。これにより、a=(d1+d2)/2=m(z1+z2)/2 という結論に達しますが、歯車の幾何学的形状(歯形修正)に調整を加える場合、わずかに異なる場合があります。.
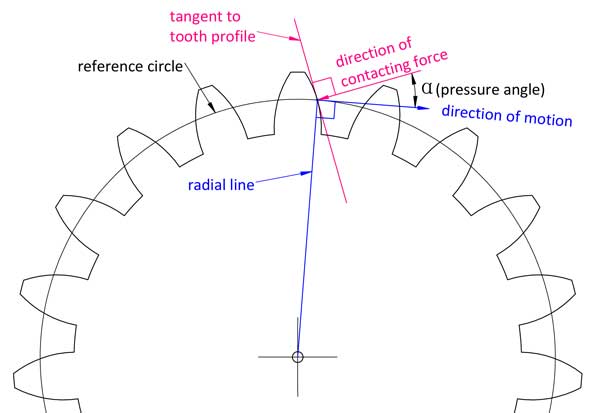
簡単に言えば、その名の通り、歯の 接触点 における接触力の方向と、その点の歯形上の運動方向との間の角度です。.
幾何学的には、インボリュート歯形の法線とその半径方向線の法線との間の角度です。.
圧力角を完全に理解したい場合は、歯形の インボリュート曲線 を理解するためにさらに深く掘り下げる必要があります。これは単に説明を簡単にする方法です。.
歯形上の異なる点では圧力角が異なりますが、歯車の圧力角について話すとき、通常は基準円上のものを指します。ほとんどの歯車は圧力角として20°を使用し、一部は14.5°または25°です。2つの噛み合う歯車は、同じモジュールと圧力角を持たなければなりません。.
6. 最小歯数 (z最小) ギアにおけるアンダーカットなし
歯車の歯数を自由に設定することはできません。歯数が少なすぎると、歯の底部が限界点を下回り、その結果、歯切り工具で歯が作られる際に、歯元の過剰な部分が切り取られることになります。.
7. プロファイルシフト係数 (x)
通常、歯形については、歯先高さ ha=1*m、歯元高さ hf=1.25*m ですが、歯形は少し上下に移動させることができます:
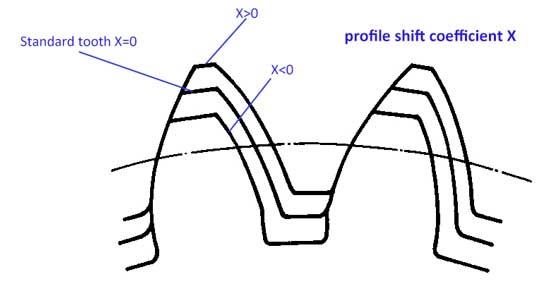

次に、歯先修正係数(x)があります。歯形が上方に移動すると、xの値は正(x>0)になり、歯形が下方に移動すると、xの値は負(x<0)になります。.
歯形の移動により、現在は以下のようになります:
- 歯先高さ ha=(1+x)*m
- 歯元高さ hf=(1.25-x)*m
歯高 h=ha+hf=2.25*m であり、標準歯車と同じままです。.
プロファイルシフトの主な理由は以下の通りです:
1) プロファイルシフトを行うことで、歯数が少なくても歯のアンダーカットを回避できます。式は以下の通りです:
xmin=(17-z)/17
例えば、歯数を14にしたい場合、X=(17-14)/17=0.176
2) 中心距離の微調整
a=[(m+x1)z1+(m+x2)z2]/2 となるため、中心距離は必ずしも (z1+z2)*m である必要はありません。
3) ピニオンをより強くします。通常、ピニオンは歯車よりも先に故障しますが、正のプロファイルシフトを加えることで、ピニオンの底部が広くなり(一方、先端は狭くなる)、より強くなります。.
要約:
| # | 項目 | 記号 | フォーミュラ |
|---|---|---|---|
| 1 | 歯数 | z | |
| 2 | モジュール | m | m=ピッチ/π |
| 3 | 歯車比 | i | i=d2/d1=z2/z1 1: 駆動ギア、2: 従動ギア |
| 4 | 歯先係数 | da* | da*=1+x 標準歯車では x=0 |
| 5 | 歯元係数 | df* | df*=1.25-x |
| 6 | 転位係数 | x | 標準歯車では x=0 |
| 7 | 圧力角 | α | 多くの歯車で α=20° その他、あまり使用されないものとして14.5°と25°があります。. |
| 8 | 基準円直径 | d | d=mz |
| 9 | 歯先円直径 | da | da=d+2Ha* x m, da=(z+2ha*) m 標準ギアの場合、da=(z+2) x m |
| 10 | 歯元円直径 | df | df=d-2Hf* x m, df=(z-2hf*) x m 標準ギアの場合、df=(z-2.5) x m |
| 11 | 歯先高さ | ha | ha=m x ha* 標準歯車では ha=m |
| 12 | 歯元高さ | hf | hf=m x hf* 標準ギアの場合、hf=1.25m |
| 13 | 歯高さ | h | h=m x (ha*+hf*) ほとんどのギアで ha*+Hf*=2.25 |
| 14 | 中心距離 | a | 標準ギアの場合、a=m x (z1+z2)/2 転位歯車の場合、a=[(m+x1)z1+(m+x2)z2]/2 |
| 15 | 根切りのない最小歯数 | Zmin | Zmin=2ha*/sinα^2 ha*=1、α=20°の場合、Zmin=17 |
| 16 | 根切りのない最小転位置 | Xmin | Xmin=(17-z)/17 |
よくある質問
ギア力の概要
2つの歯車が噛み合う過程において、駆動側歯車が被駆動側歯車に及ぼす力は、被駆動側歯車の歯面に垂直な法線力と、その法線力に垂直な接線力に分解できます。接線力は被駆動側歯車を駆動する役割を果たさず、両歯車間の摩耗を引き起こします。駆動側と被駆動側の歯車の噛み合い点における角度は、噛み合いの開始時と終了時に最も大きく、中間では小さくなります。噛み合い点が両歯車の中心線上にあるとき、その角度はゼロになります。したがって、角度を小さくすることで伝達効率を向上させ、摩耗を低減することができます。.
圧力角とかみあい角の関係
圧力角は噛み合い角と直接関係しています。一方、圧力角を小さくすると歯元が薄くなり、歯車の強度が低下します。したがって、バランスを見つけることが重要です。.
歯車圧力角の工業規格
- 現在の工業生産では、ほとんどの標準歯車は20°の圧力角を使用しています。.
- 軽負荷・高速用に設計された歯車は、14.5°の圧力角を使用することが多く、騒音が低く伝動効率が高いという利点があります。.
- 低速・高負荷用途向けに設計された歯車は、25°の圧力角を使用し、歯の強度が高い反面、伝動効率が低く騒音が大きくなるというトレードオフがあります。.
プラスチック歯車
プラスチック製の歯車の場合、製造に標準的な切削工具を必要としないため、任意の圧力角を選択できます。ただし、設計を簡素化するために、これらの標準値に従うことが一般的です。.
円周円は歯車計算の基礎となります。その直径は、モジュール(m)に歯数(Z)を乗じて計算されます。本質的に、これは主に計算に使用される理論上の円であり、他の歯車パラメータはこれから導出されます。.
一方、ピッチ円直径は、2つの歯車が実際に噛み合う際に定義されます。これは、歯車の共通法線とそれらの中心を結ぶ線の交点によって形成され、接点を通る円です。噛み合う2つの歯車のピッチ円は互いに接しています。ただし、円周円が常に接しているとは限りません。
標準的な歯車設計では、円周円とピッチ円は通常一致します。しかし、バックラッシュを増やすために中心距離を調整した場合や、歯車が修正されている場合、円周円とピッチ円は異なることがあります。.
はい。標準設計では、円周円上の歯厚と溝幅は等しくなります。.
しかし、実際の応用では、標準の中心距離を維持しながらある程度のバックラッシュを確保するために、歯厚をわずかに薄くすることがあります。.
一つの方法は、円周円上の歯厚を溝幅よりわずかに小さくすることです。.
別の方法は、歯車を標準よりわずかに大きい中心距離で取り付けることです。.
必要なバックラッシュの大きさは、歯車の製造精度に依存します。精度が高いほど、バックラッシュの必要性は低減されます。.
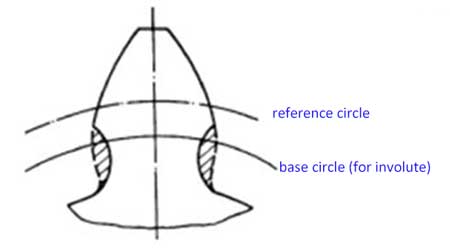
歯車の基礎円は、そのインボリュートが生成される円です。そのピッチは、基礎円上の隣接する2つの歯の歯形上の同一ポイント間の弧長であり、したがって:
Pb = Db/Z.
ここで、Dbは基礎円の直径です。.
または Pb = Df * cos(α) / Z = mπ * cos(α),
ここで、Dfは円周円の直径、mは歯車のモジュール、αは円周円の圧力角です。.
1. 平歯車の場合、一組の歯の噛み合いが前の組の噛み合いと同期していることが求められます。これは、それらの基礎円ピッチが等しいことを意味し、すなわち:
m1 * cos(α1) = m2 * cos(α2).
これから、噛み合う一対の歯車のモジュール(m)が必ずしも等しくなくてもよいことが推測できます。.
2. 同時に、重なり係数(接触率ε)は1より大きい必要があります。
標準的な切削工具で製造された歯車の場合、工具の標準化と系列化により、両歯車に同じモジュールと円周円圧力角を使用することが一般的な慣行です。.
3. はすば歯車の場合、取り付け軸が平行であると仮定すると、それらのねじれ角も等しい必要があります。.
接触率(ε)は、噛み合う2つの歯車の共通法線セグメントの長さを、歯車の基礎ピッチ(Pb)で割った値であり、そのセグメントは歯車の歯先円によって切り取られます。.
- ε <1の場合、歯が接触していない瞬間があるため、ギアは正しく機能しません。.
- 1 < ε < 2 の場合、1つの歯だけが接触している時間があります。例えば、ε = 1.63 の場合、平均して1.63組の歯がかみあっていると想像できます。伝動過程の37%の時間では1つの歯のみがかみあい、63%の時間では2つの歯がかみあうため、伝動中の衝撃が大きくなります。.
- ε > 2 の場合、任意の時点で2組以上の歯が接触しているため、伝動がより滑らかになります。.
歯車の歯数(Z)は、接触率に影響を与える重要な要素です。.
小さな歯車では、接触率を高めるためにしばしばはすば歯車が使用されます。しかし、はすば歯車の製造コストは平歯車よりも大幅に高くなります。.
別の方法として、ピッチ円の圧力角を小さくする方法がありますが、その効果は限定的です。.
歯車の寿命は主に摩耗と疲労破壊によって決まります。これらの問題は、歯車精度の低さ、不適切なバックラッシュ、潤滑不良、過熱など、さまざまな要因に起因します。経験式で寿命を計算することは困難ですが、歯車の精度と使用材料はその寿命にとって重要な要素です。.



コメントは受け付けていません。