Índice
ToggleEsta es una versión más sencilla de la terminología de los engranajes y las fórmulas de cálculo de los dientes
Este post pretende explicar la terminología de los engranajes y las fórmulas de cálculo de los dientes de una forma más sencilla para los principiantes, y también para aquellos que han aprendido engranajes hace tiempo pero quieren retomarlos rápidamente.
Los engranajes tienen muchos parámetros que requerirán un poco de matemáticas y formación geométrica para entenderlos completamente. Sin embargo, no es necesario profundizar demasiado en los conceptos básicos del conocimiento de engranajes, después de haber leído este post, usted debe ser capaz de hacer diseños preliminares de engranajes o tener una comunicación efectiva con los diseñadores de engranajes.
Empecemos por la forma de engranaje básica, los engranajes rectos:
Contenido
1. Número de dientes (z); 2. Círculo de referencia y diámetro de referencia (d); 3. 3. Módulo (m); 4. Distancia al centro (a). Número mínimo de dientes (zmin); 7.Coeficiente de desplazamiento del perfil (x); 8. Tabla resumen.
1. Número de dientes (z)
Esto es bastante sencillo, es el número de dientes del engranaje.
2. Círculo de referencia y diámetro de referencia (d)
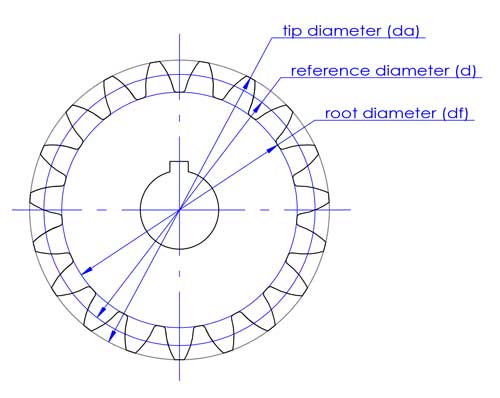
El diámetro de la punta (da) y el diámetro de la raíz (df) corresponden a la parte superior e inferior de los dientes.
El diámetro de referencia se utiliza en el diseño y cálculo de engranajes. Tiene conexiones directas con otros parámetros importantes del engranaje como el módulo (m), la distancia entre ejes (c) y el ángulo de presión (α).
El diámetro de la punta (da) y el diámetro de la raíz (df) corresponden a la parte superior e inferior de los dientes.
El diámetro de referencia se utiliza en el diseño y cálculo de engranajes. Tiene conexiones directas con otros parámetros importantes del engranaje como el módulo (m), la distancia entre ejes (c) y el ángulo de presión (α).
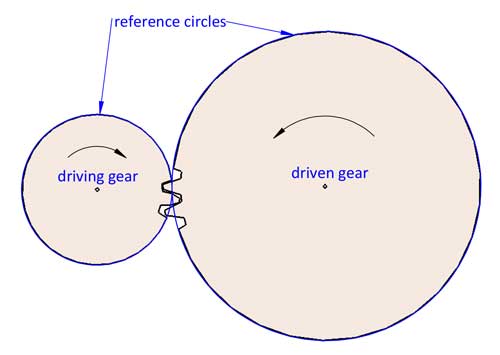
El giro de 2 ruedas dentadas puede considerarse el giro acoplado de 2 círculos de referencia sin deslizamiento. La relación de transmisión i=d2/d1. d1 y d2 se refieren a los diámetros de referencia de 2 ruedas dentadas acopladas (la rueda 1 es la rueda motriz y la rueda 2 es la rueda conducida).

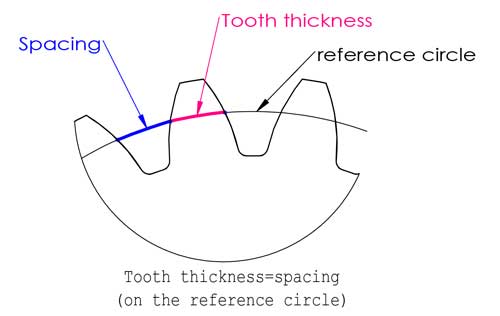
El círculo de referencia se encuentra en algún punto entre la punta y la base de los dientes, normalmente es donde el grosor del diente es igual al espaciado, pero no siempre es así (hablaremos del desplazamiento del perfil más adelante en este post).
3. Módulo (m)
El módulo es probablemente el parámetro de engranaje más importante, y aparece casi siempre en las fórmulas de cálculo de dientes. En realidad, no es tan difícil de entender como podría imaginarse. Primero entendamos qué es el paso, El paso es la longitud de arco entre los puntos correspondientes de dientes adyacentes, normalmente en el círculo de referencia.
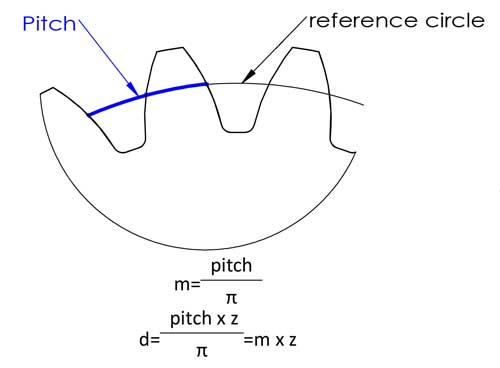

Entonces tenemos el diámetro de referencia d=circunferencia/π=pitch*z/π, para facilitar el cálculo, definimos el pitch/π como el módulo, y ahora tenemos la ecuación de d=m*z, esto facilita mucho el cálculo, ¿verdad? Los módulos se han estandarizado en los siguientes números (unidad: mm):
Primera serie (recomendada): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Segunda serie (menos utilizada): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Sin embargo, en el caso de los engranajes de plástico moldeados por inyección, no es necesario adoptar estos números de módulo estándar, ya que los dientes no se cortan con talladoras de dientes estándar.
Ahora tenemos la relación de transmisión i=d2/d1=z2/z1 (la marcha 1 es la marcha motriz y la marcha 2 es la marcha conducida).
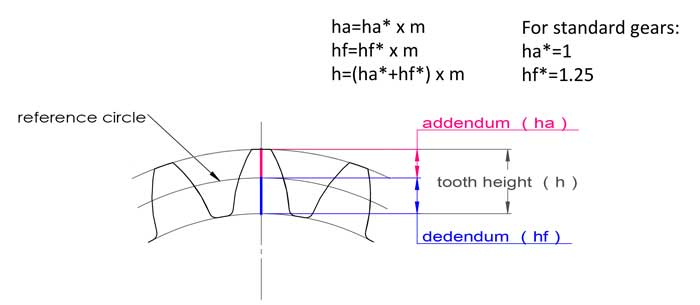
El módulo también tiene que ver con la altura del diente, para los engranajes estándar, la altura del diente es igual a 2,25*m:
addendum ha=1*m, dedendum hf=1,25*m, altura del diente h=2,25*m.
4. Distancia entre ejes (a)
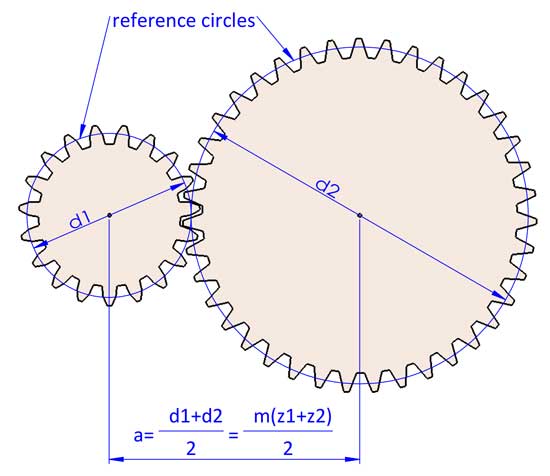
2 engranajes que engranan siempre tienen el mismo módulo de lo contrario no coinciden. Ahora podemos llegar a la conclusión de que a=(d1+d2)/2=m(z1+z2)/2, pero puede ser ligeramente diferente haciendo algunos ajustes en las geometrías de los engranajes (desplazamiento del perfil de los dientes).
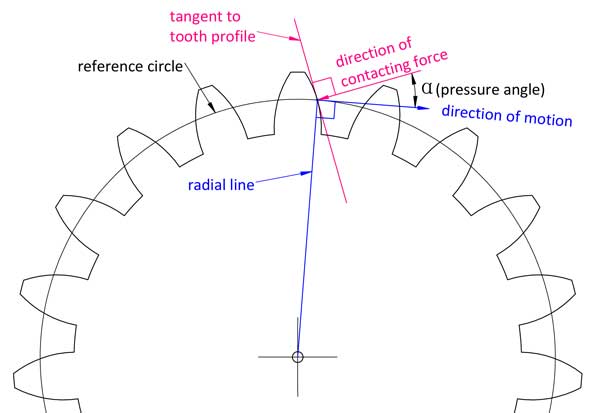
En pocas palabras, como su nombre indica, es el ángulo entre la dirección de la fuerza de contacto sobre el punto de contacto del diente y la dirección de movimiento de ese punto sobre el perfil del diente.
En geometría, es el ángulo entre la línea normal al perfil del diente evolvente y la línea normal a su línea radial.
Si quieres entender completamente el ángulo de presión entonces necesitas profundizar para entender la línea involuta del perfil del diente. Esto es sólo una forma más fácil de explicación.
Diferentes puntos del perfil del diente tienen diferentes ángulos de presión, pero cuando hablamos del ángulo de presión de una rueda dentada, normalmente nos referimos al del círculo de referencia. La mayoría de los engranajes utilizan 20° como ángulo de presión, algunos tienen 14,5° o 25°. 2 engranajes acoplados deben tener el mismo módulo y ángulo de presión.
6. Número mínimo de dientes (zmin) sin socavar la marcha
No se puede tener cualquier número de dientes del engranaje como se desee. Si hay muy pocos dientes, la parte inferior de los dientes estará por debajo del punto límite, como consecuencia, cuando los dientes se hacen por los cortadores de dientes, una parte sobrante de la raíz de los dientes se cortará.
7. Coeficiente de desplazamiento del perfil (x)
Normalmente para el perfil de los dientes, el addendum de los dientes ha=1*m, y el dedendum hf=1.25*m, sin embargo el perfil de los dientes puede moverse un poco hacia arriba o hacia abajo:
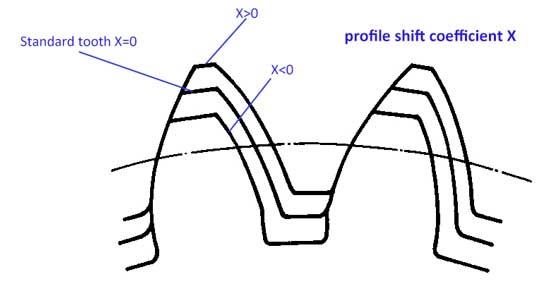

Ahora tenemos el coeficiente de desplazamiento del perfil (x). Cuando el perfil se desplaza hacia arriba, el valor de x es positivo (x>0), y si el perfil se desplaza hacia abajo, el valor de x es negativo (x<0).
Con el movimiento de perfil de los dientes, ahora tenemos:
- addendum ha=(1+x)*m
- dedendum hf=(1,25-x)*m
La altura de los dientes h=ha+hf=2,25*m, sigue siendo la misma que la de los dientes estándar.
Las principales razones del cambio de perfil son:
1) Con el perfil desplazado, podemos evitar la socavación de los dientes con un menor número de dientes. La fórmula es la siguiente:
xmin=(17-z)/17
Por ejemplo, si desea que el número de dientes sea 14, entonces X=(17-14)/17=0,176
2)Ajuste fino de la distancia entre ejes
a=[(m+x1)z1+(m+x2)z2]/2, por lo que la distancia al centro no tiene por qué ser (z1+z2)*m
3)Hacer el piñón más fuerte. Por lo general, el piñón falla antes de la marcha, mediante la adición de un cambio de perfil positivo, la parte inferior del piñón se hace más ancha (mientras que la punta se hace más estrecha) por lo que es más fuerte.
En resumen:
| # | Artículo | Símbolo | Fórmula |
|---|---|---|---|
| 1 | número de dientes | z | |
| 2 | módulo | m | m=pitch/π |
| 3 | relación de transmisión | i | i=d2/d1=z2/z1 1: engranaje motriz, y 2: engranaje conducido |
| 4 | coeficiente de adición | da* | da*=1+x x=0 para marchas estándar |
| 5 | coeficiente dedendum | df* | df*=1,25-x |
| 6 | coeficiente de desplazamiento del perfil | x | Para los engranajes estándar,, x=0 |
| 7 | ángulo de presión | α | α=20° para la mayoría de las marchas Otros menos utilizados son 14,5° y 25°. |
| 8 | diámetro de referencia | d | d=mz |
| 9 | diámetro de la punta | da | da=d+2Ha* x m, da=(z+2ha*) m Para los engranajes normalizados, da=(z+2) x m |
| 10 | diámetro de la raíz | df | df=d-2Hf* x m, df=(z-2hf*) x m Para los engranajes estándar, df=(z-2,5) x m |
| 11 | adenda | ha | ha=m x ha* Para los engranajes estándar, ha=m |
| 12 | dedendum | hf | hf=m x hf* Para marchas estándar, hf=1,25m |
| 13 | altura del diente | h | h=m x (ha*+hf*) ha*+Hf*=2,25 para la mayoría de las marchas |
| 14 | distancia entre centros | a | a=m x (z1+z2)/2 para marchas estándar a=[(m+x1)z1+(m+x2)z2]/2 para marchas desplazadas de perfil |
| 15 | Número mínimo de dientes sin socavar | Zmin | Zmin=2ha*/sinα^2 Zmin=17 cuando ha*=1, α=20°. |
| 16 | Desplazamiento mínimo del perfil sin socavación | Xmin | Xmín=(17-z)/17 |
Preguntas frecuentes
Introducción a las fuerzas de engranaje
En el proceso de engrane entre dos engranajes, la fuerza ejercida por el engranaje motriz sobre el engranaje conducido puede descomponerse en una fuerza normal perpendicular a la superficie del engranaje conducido y una fuerza tangencial perpendicular a la fuerza normal. La fuerza tangencial no participa en el accionamiento del engranaje conducido y provoca el desgaste entre los dos engranajes. El ángulo en el punto de engrane de las ruedas motriz y conducida es mayor al principio y al final del engrane y menor en el centro. Cuando el punto de engrane está en la línea central de los dos engranajes, es igual a cero. Por lo tanto, un ángulo menor puede mejorar la eficacia de la transmisión y reducir el desgaste.
Relación entre el ángulo de presión y el ángulo de mallado
El ángulo de presión está directamente relacionado con el ángulo de engrane. Por otra parte, un ángulo de presión menor da lugar a raíces de engranaje más delgadas, lo que reduce la resistencia de los engranajes. Por tanto, es importante encontrar un equilibrio.
Normas industriales para ángulos de presión de engranajes
- En la producción industrial actual, la mayoría de los engranajes estándar utilizan un ángulo de presión de 20°.
- Los engranajes diseñados para cargas ligeras y altas velocidades suelen utilizar un ángulo de presión de 14,5°, que presenta las ventajas de un menor ruido y una mayor eficacia de transmisión.
- Los engranajes diseñados para aplicaciones de baja velocidad y carga pesada utilizan un ángulo de presión de 25°, que ofrece una mayor resistencia del diente pero a costa de una menor eficacia de la transmisión y un mayor ruido.
Engranajes de plástico
En el caso de los engranajes de plástico, puede elegirse cualquier ángulo de presión, ya que para su fabricación no se requieren herramientas de corte estándar. Sin embargo, para simplificar el diseño, es habitual ceñirse a estos valores estándar.
El círculo circunferencial es la base para el cálculo de engranajes. Su diámetro se calcula como el módulo (m) multiplicado por el número de dientes (Z). Esencialmente, es un círculo teórico que se utiliza principalmente para los cálculos, y del que se derivan otros parámetros de los engranajes.
En cambio, el diámetro de paso se define durante el engrane real de dos ruedas dentadas. Es el círculo formado por la intersección de la normal común de los engranajes y la línea que une sus centros, pasando por el punto de tangencia. Los círculos de paso de dos ruedas dentadas engranadas son tangentes entre sí. Sin embargo, los círculos de circunferencia pueden no ser siempre tangentes
En los diseños de engranajes estándar, el círculo de circunferencia y el círculo de paso suelen coincidir. Sin embargo, si la distancia entre ejes se ajusta para aumentar el juego o si los engranajes se han modificado, el círculo periférico y el círculo primitivo pueden diferir.
Sí. En los diseños estándar, el grosor del diente y la anchura de la ranura en el círculo de la circunferencia son iguales.
Sin embargo, en aplicaciones prácticas, para permitir cierto juego manteniendo la distancia entre ejes estándar, el espesor del diente se hace ligeramente más fino.
Un método consiste en hacer que el grosor del diente sea ligeramente inferior a la anchura de la ranura en el círculo de la circunferencia.
Otro método consiste en instalar los engranajes a una distancia entre ejes ligeramente superior a la estándar.
El tamaño necesario de la holgura depende de la precisión de fabricación de los engranajes; una mayor precisión reduce la necesidad de holgura.
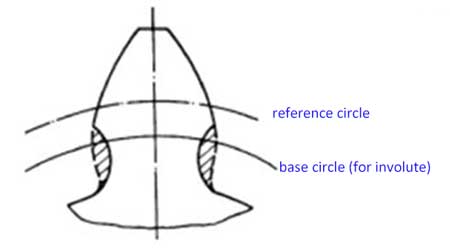
El círculo de base de un engranaje es el círculo a partir del cual se genera su evolvente. Su paso es la longitud de arco entre puntos idénticos de los perfiles de dos dientes adyacentes en el círculo base, así:
Pb = Db/Z.
Aquí, Db es el diámetro del círculo base.
O Pb = Df * cos(α) / Z = mπ * cos(α),
donde Df es el diámetro del círculo de circunferencia, m es el módulo del engranaje y α es el ángulo de presión del círculo de circunferencia.
1. Para los engranajes rectos, es necesario que el engrane de un par de dientes esté sincronizado con el engrane del par anterior. Esto exige que los pasos de sus círculos base sean iguales, es decir:
m1 * cos(α1) = m2 * cos(α2).
De ello se deduce que los módulos (m) de un par de engranajes no tienen por qué ser necesariamente iguales.
2. Al mismo tiempo, el grado de compromiso (relación de contacto ε) es superior a 1
Para los engranajes fabricados con herramientas de corte estándar, debido a la normalización y serialización de las herramientas, es práctica común utilizar el mismo módulo y ángulo de presión del círculo de circunferencia para ambos engranajes.
3. Para los engranajes helicoidales, también es necesario que sus ángulos de hélice sean iguales, suponiendo que sus ejes de instalación sean paralelos.
La relación de contacto (ε) es la longitud del segmento normal común entre dos ruedas dentadas que engranan, cortada por los círculos de adición de las ruedas dentadas, dividida por el paso base (Pb) de la rueda dentada.
- Cuando ε <1, los engranajes no pueden funcionar correctamente porque hay momentos en los que ningún diente está en contacto.
- Si 1 < ε < 2, hay momentos en los que sólo un diente está en contacto. Por ejemplo, con ε = 1,63, se puede imaginar una media de 1,63 pares de dientes engranados. Durante 37% del proceso de transmisión, sólo un diente está en contacto, mientras que durante 63%, dos dientes están en contacto, lo que provoca un mayor impacto durante la transmisión.
- Si ε > 2, en un momento dado hay más de dos pares de dientes en contacto, lo que se traduce en una transmisión más suave.
El número de dientes (Z) de los engranajes es un factor importante que afecta a la relación de contacto.
En el caso de los engranajes más pequeños, se suelen utilizar engranajes helicoidales para aumentar la relación de contacto. Sin embargo, el coste de fabricación de los engranajes helicoidales es significativamente mayor que el de los engranajes rectos.
Otro método consiste en utilizar un ángulo de presión menor del círculo de cabeceo, pero esto tiene un efecto menor.
La vida útil de un engranaje viene determinada principalmente por el desgaste y la rotura por fatiga. Estos problemas se derivan de diversos factores, como la baja precisión del engranaje, un juego inadecuado, una lubricación deficiente, el sobrecalentamiento, etc. Aunque es difícil calcular la vida útil con fórmulas empíricas, la precisión del engranaje y el material utilizado son factores críticos para su longevidad.



Los comentarios están cerrados.