فهرست مطالب
تغییر وضعیتاین نسخه سادهتری از اصطلاحات چرخدنده و فرمولهای محاسبه دندانه است
این پست برای توضیح اصطلاحات چرخدنده و فرمولهای محاسبه دندانهها به روشی سادهتر برای مبتدیان، و همچنین برای کسانی که مدتی پیش چرخدندهها را یاد گرفتهاند و میخواهند به سرعت دوباره مرور کنند، است.
دندهها پارامترهای زیادی دارند که برای درک کامل آنها به کمی ریاضیات و آموزش هندسی نیاز است. با این حال، شما نیازی به عمیق شدن در مفاهیم پایه دانش دنده ندارید، پس از خواندن این پست، باید بتوانید طراحیهای اولیه دنده را انجام دهید یا ارتباط مؤثری با طراحان دنده برقرار کنید.
بیایید از شکل پایه چرخدنده، یعنی چرخدندههای ساده شروع کنیم:
فهرست مطالب
1. تعداد دندانه (z)؛ 2. دایره مبنا و قطر مبنا (d)؛ 3. مدول (m)؛ 4. فاصله مراکز (a)؛ 5. زاویه فشار (α)؛ 6. حداقل تعداد دندانه (zmin)؛ 7. ضریب جابجایی پروفیل (x)؛ 8. جدول خلاصه.
1. تعداد دندانها (z)
این کاملاً سرراست است، تعداد دندانههای چرخدنده است.
2. دایره مرجع و قطر مرجع (d)
قطر نوک (da) و قطر ریشه (df) به ترتیب با بالاترین و پایینترین نقطه دندانهها مطابقت دارند.
قطر مرجع در طراحی و محاسبه چرخدنده استفاده میشود. این قطر ارتباط مستقیمی با پارامترهای مهم دیگر چرخدنده مانند مدول (m)، فاصله مراکز (c) و زاویه فشار (α) دارد.
قطر نوک (da) و قطر ریشه (df) به ترتیب با بالاترین و پایینترین نقطه دندانهها مطابقت دارند.
قطر مرجع در طراحی و محاسبه چرخدنده استفاده میشود. این قطر ارتباط مستقیمی با پارامترهای مهم دیگر چرخدنده مانند مدول (m)، فاصله مراکز (c) و زاویه فشار (α) دارد.
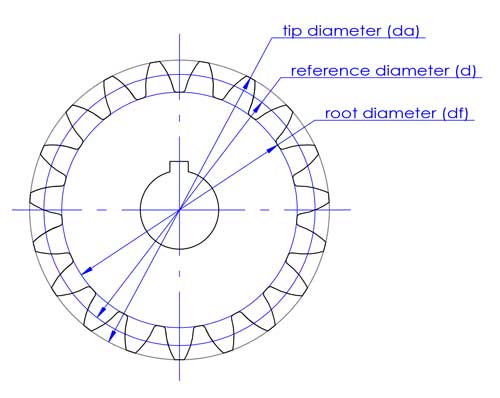
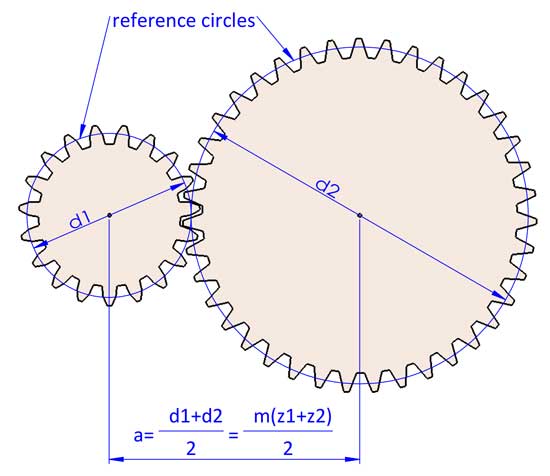
چرخش دو چرخدنده را میتوان به عنوان چرخش درگیر دو دایره مرجع بدون لغزش در نظر گرفت. نسبت چرخدنده i=d2/d1 است. d1 و d2 به قطرهای مرجع دو چرخدنده درگیر اشاره دارند (چرخدنده 1 چرخدنده محرک و چرخدنده 2 چرخدنده متحرک است).
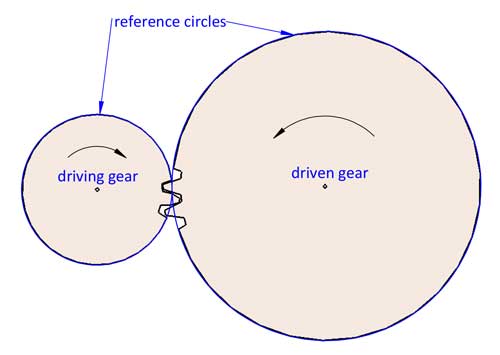

دایره مرجع جایی بین نوک و پایین دندانهها قرار دارد، معمولاً جایی است که ضخامت دندانه با فاصله برابر است، اما این همیشه اینطور نیست (بعداً در این پست در مورد جابجایی پروفیل صحبت خواهیم کرد).
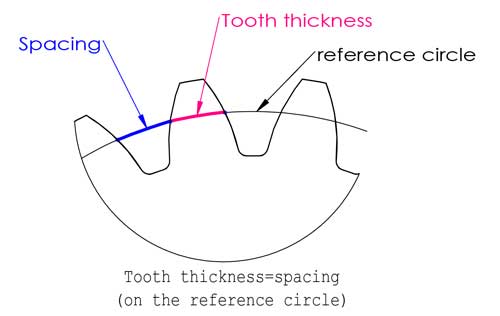
3. مدول (m)
مدول احتمالاً مهمترین پارامتر چرخدنده است و تقریباً در همه فرمولهای محاسبه دندانهها ظاهر میشود. در واقع، درک آن آنقدرها هم که ممکن است تصور کنید دشوار نیست. ابتدا بیایید بفهمیم گام چیست، گام طول کمان بین نقاط متناظر روی دندانههای مجاور است، معمولاً روی دایره مرجع.
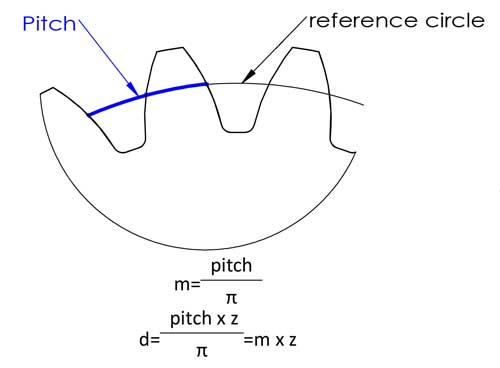

سپس قطر مبنا را داریم d=محیط/π=گام*z/π، برای آسانتر کردن محاسبه، گام/π را به عنوان مدول تعریف میکنیم، و اکنون معادله d=m*z را داریم، این محاسبه را بسیار آسانتر میکند، درست است؟ مدولها در اعداد زیر استاندارد شدهاند (واحد: میلیمتر):
سری اول (توصیه شده): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
سری دوم (کمتر استفاده میشود): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
با این حال، برای چرخدندههای پلاستیکی تزریقی، نیازی به اتخاذ این اعداد استاندارد مدول نیست، زیرا دندانهها با ابزارهای برش استاندارد بریده نمیشوند.
اکنون نسبت چرخدنده i=d2/d1=z2/z1 را داریم (چرخدنده 1 چرخدنده محرک و چرخدنده 2 چرخدنده متحرک است).
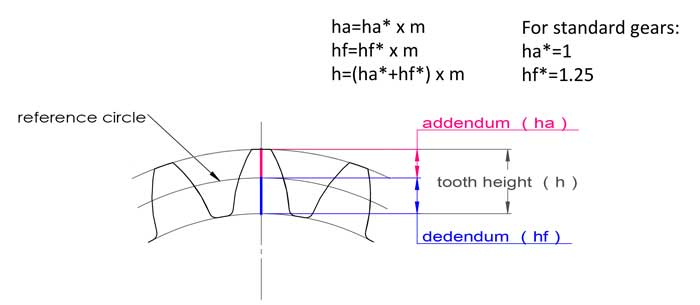
مدول همچنین با ارتفاع دندانه مرتبط است، برای چرخدندههای استاندارد، ارتفاع دندانه برابر با 2.25*m است:
ارتفاع سر دندانه ha=1*m، ارتفاع پای دندانه hf=1.25*m، ارتفاع دندانه h=2.25*m.
4. فاصله مرکز (a)
2 دنده درگیر همیشه مدول یکسانی دارند در غیر این صورت با هم مطابقت ندارند. اکنون میتوانیم به این نتیجه برسیم که a=(d1+d2)/2=m(z1+z2)/2، اما میتواند کمی متفاوت باشد در حالی که برخی تنظیمات روی هندسه دنده (جابجایی پروفیل دندانه) انجام میشود.
به زبان ساده، همانطور که از نامش پیداست، زاویه بین جهت نیروی تماس در نقطه تماس دندانه و جهت حرکت آن نقطه روی پروفیل دندانه است.
در هندسه، این زاویه بین خط عمود بر پروفیل دندانه اینولوت و خط عمود بر خط شعاعی آن است.
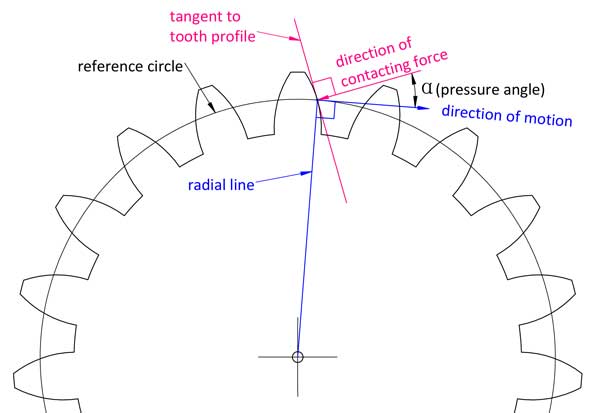
اگر میخواهید زاویه فشار را به طور کامل درک کنید، باید عمیقتر بروید تا خط اینولوت پروفیل دندانه را درک کنید. این فقط یک روش سادهتر برای توضیح است.
نقاط مختلف روی پروفیل دندانه زوایای فشار متفاوتی دارند، اما وقتی در مورد زاویه فشار یک چرخدنده صحبت میکنیم، معمولاً به آن روی دایره مرجع اشاره میشود. بیشتر چرخدندهها از 20° به عنوان زاویه فشار استفاده میکنند، برخی 14.5° یا 25° هستند. دو چرخدنده درگیر باید مدول و زاویه فشار یکسانی داشته باشند.
6. حداقل تعداد دندان (zحداقل) بدون برش زیرین در چرخدنده
شما نمیتوانید هر تعداد دندانهای که میخواهید برای چرخدنده داشته باشید. اگر تعداد دندانهها خیلی کم باشد، پایین دندانهها زیر نقطه حد خواهد بود، در نتیجه، وقتی دندانهها با ابزارهای برش ساخته میشوند، بخش اضافی ریشه دندانه بریده خواهد شد.
7. ضریب تغییر پروفایل (x)
معمولاً برای پروفیل دندانه، ارتفاع سر دندانه ha=1*m و ارتفاع پایه دندانه hf=1.25*m است، با این حال پروفیل دندانه میتواند کمی به بالا یا پایین جابجا شود:
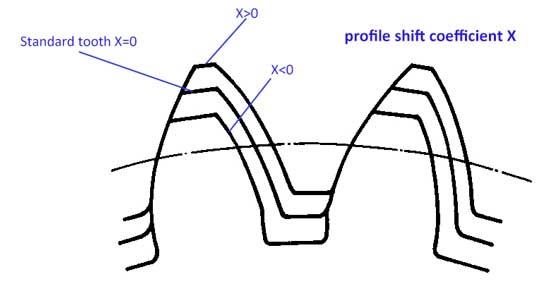

اکنون ضریب جابجایی پروفیل (x) را داریم. هنگامی که پروفیل به سمت بالا جابجا میشود، مقدار x مثبت است (x>0)، و اگر پروفیل به سمت پایین جابجا شود، مقدار x منفی است (x<0).
با جابجایی پروفیل دندانه، اکنون داریم:
- سر دندان ha=(1+x)*m
- ریشه دندان hf=(1.25-x)*m
ارتفاع دندانه h=ha+hf=2.25*m، که همچنان مانند دندانههای استاندارد است.
دلایل اصلی تغییر پروفایل عبارتند از:
1) با جابجایی پروفیل، میتوانیم از برش زیرین دندانه با تعداد دندانه کمتر جلوگیری کنیم. فرمول به شرح زیر است:
xmin=(17-z)/17
به عنوان مثال، اگر میخواهید تعداد دندانهها 14 باشد، آنگاه X=(17-14)/17=0.176
2) تنظیم دقیق فاصله مرکز
a=[(m+x1)z1+(m+x2)z2]/2، بنابراین فاصله مراکز لزوماً (z1+z2)*m نیست
3) قویتر کردن پینیون. معمولاً پینیون قبل از چرخدنده خراب میشود، با افزودن جابجایی پروفیل مثبت، پایین پینیون پهنتر میشود (در حالی که نوک باریکتر میشود) و در نتیجه آن را قویتر میکند.
به طور خلاصه:
| # | مورد | نماد | فرمول |
|---|---|---|---|
| 1 | تعداد دندان | z | |
| 2 | مدول | m | m=pitch/π |
| 3 | نسبت چرخ دنده | i | i=d2/d1=z2/z1 1: چرخدنده محرک، و 2: چرخدنده متحرک |
| 4 | ضریب سر دندان | da* | da*=1+x x=0 برای چرخ دنده های استاندارد |
| 5 | ضریب ریشه دندان | df* | df*=1.25-x |
| 6 | ضریب جابجایی پروفیل | x | برای چرخ دنده های استاندارد، x=0 |
| 7 | زاویه فشار | α | α=20° برای اکثر چرخ دنده ها دیگر موارد کمتر استفاده شده 14.5° و 25° هستند. |
| 8 | قطر مرجع | d | d=mz |
| 9 | قطر نوک | da | da=d+2Ha* x m، da=(z+2ha*) m برای چرخدندههای استاندارد، da=(z+2) x m |
| 10 | قطر ریشه | df | df=d-2Hf* x m، df=(z-2hf*) x m برای چرخدندههای استاندارد، df=(z-2.5) x m |
| 11 | سر دندان | ha | ha=m x ha* برای چرخ دنده های استاندارد، ha=m |
| 12 | ریشه دندان | hf | hf=m x hf* برای چرخدندههای استاندارد، hf=1.25m |
| 13 | ارتفاع دندان | h | h=m x (ha*+hf*) ha*+Hf*=2.25 برای اکثر چرخدندهها |
| 14 | فاصله مرکز | a | a=m x (z1+z2)/2 برای چرخدندههای استاندارد a=[(m+x1)z1+(m+x2)z2]/2 برای چرخدندههای با تغییر پروفیل |
| 15 | حداقل تعداد دندانه بدون برش زیرین | Zmin | Zmin=2ha*/sinα^2 Zmin=17 وقتی ha*=1، α=20° |
| 16 | حداقل تغییر پروفیل بدون برش زیرین | Xmin | Xmin=(17-z)/17 |
سوالات متداول
مقدمهای بر نیروهای چرخدنده
در فرآیند درگیر شدن دو چرخدنده، نیروی اعمال شده توسط چرخدنده محرک بر چرخدنده متحرک را میتوان به یک نیروی عمودی بر سطح چرخدنده متحرک و یک نیروی مماسی عمود بر نیروی عمودی تجزیه کرد. نیروی مماسی در به حرکت درآوردن چرخدنده متحرک مشارکت نمیکند و باعث سایش بین دو چرخدنده میشود. زاویه در نقطه درگیری چرخدندههای محرک و متحرک در ابتدا و انتهای درگیری بیشترین مقدار و در وسط کمتر است. هنگامی که نقطه درگیری روی خط مرکزی دو چرخدنده قرار دارد، برابر صفر است. بنابراین، زاویه کوچکتر میتواند بازده انتقال را بهبود بخشد و سایش را کاهش دهد.
رابطه بین زاویه فشار و زاویه درگیری
زاویه فشار مستقیماً با زاویه درگیری مرتبط است. از سوی دیگر، زاویه فشار کوچکتر منجر به ریشههای نازکتر چرخدنده میشود که استحکام چرخدندهها را کاهش میدهد. بنابراین، یافتن تعادل مهم است.
استانداردهای صنعتی برای زوایای فشار چرخدنده
- در تولید صنعتی فعلی، اکثر چرخدندههای استاندارد از زاویه فشار 20 درجه استفاده میکنند.
- چرخدندههای طراحیشده برای بارهای سبک و سرعتهای بالا اغلب از زاویه فشار 14.5 درجه استفاده میکنند که مزایای نویز کمتر و بازده انتقال بالاتر را دارد.
- چرخدندههای طراحیشده برای کاربردهای کمسرعت و بار سنگین از زاویه فشار 25 درجه استفاده میکنند که استحکام دندانه بالاتر را ارائه میدهد اما به قیمت بازده انتقال پایینتر و نویز بالاتر است.
چرخ دنده های پلاستیکی
برای چرخدندههای پلاستیکی، هر زاویه فشاری را میتوان انتخاب کرد زیرا برای تولید آنها به ابزارهای برش استاندارد نیاز نیست. با این حال، برای سادگی در طراحی، معمول است که به این مقادیر استاندارد پایبند بمانیم.
دایره محیطی مبنای محاسبات چرخدنده است. قطر آن به عنوان مدول (m) ضرب در تعداد دندانهها (Z) محاسبه میشود. اساساً، این یک دایره نظری است که عمدتاً برای محاسبات استفاده میشود و سایر پارامترهای چرخدنده از آن استخراج میشوند.
از سوی دیگر، قطر گام در هنگام درگیری واقعی دو چرخدنده تعریف میشود. این دایرهای است که از تقاطع عمود مشترک چرخدندهها و خط اتصال مراکز آنها تشکیل میشود و از نقطه تماس میگذرد. دایرههای گام دو چرخدنده درگیر بر یکدیگر مماس هستند. با این حال، دایرههای محیطی ممکن است همیشه مماس نباشند.
در طراحیهای استاندارد چرخدنده، دایره محیطی و دایره گام معمولاً بر هم منطبق هستند. با این حال، اگر فاصله مرکزی برای افزایش لقی تنظیم شود یا اگر چرخدندهها اصلاح شده باشند، دایره محیطی و دایره گام ممکن است متفاوت باشند.
بله. در طراحیهای استاندارد، ضخامت دندانه و عرض شیار روی دایره محیطی برابر هستند.
با این حال، در کاربردهای عملی، برای ایجاد مقداری لقی در حالی که فاصله مرکزی استاندارد حفظ میشود، ضخامت دندانه کمی نازکتر ساخته میشود.
یک روش این است که ضخامت دندانه را کمی کوچکتر از عرض شیار روی دایره محیطی بسازیم.
روش دیگر این است که چرخدندهها را در فاصله مرکزی کمی بزرگتر از استاندارد نصب کنیم.
اندازه مورد نیاز لقی به دقت ساخت چرخدندهها بستگی دارد؛ دقت بالاتر نیاز به لقی را کاهش میدهد.
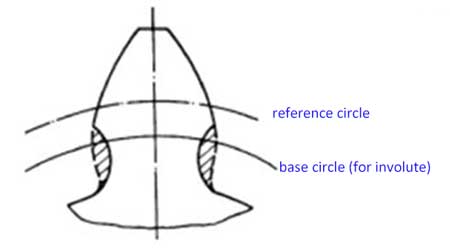
دایره پایه یک چرخدنده دایرهای است که از آن اینولوت آن ایجاد میشود. گام آن طول کمان بین نقاط یکسان روی پروفیلهای دو دندانه مجاور روی دایره پایه است، بنابراین:
Pb = Db/Z.
در اینجا، Db قطر دایره پایه است.
یا Pb = Df * cos(α) / Z = mπ * cos(α)،,
که در آن Df قطر دایره محیطی، m مدول چرخدنده و α زاویه فشار دایره محیطی است.
1. برای چرخدندههای ساده، لازم است که درگیری یک جفت دندانه با درگیری جفت قبلی همگام باشد. این مستلزم آن است که گامهای دایره پایه آنها برابر باشند، به این معنی که:
m1 * cos(α1) = m2 * cos(α2).
از این میتوان استنباط کرد که مدولهای (m) یک جفت چرخدنده درگیر لزوماً نباید برابر باشند.
2. در عین حال، درجه درگیری (نسبت تماس ε) بزرگتر از 1 است.
برای چرخدندههای ساخته شده با ابزارهای برش استاندارد، به دلیل استانداردسازی و سریسازی ابزارها، معمول است که از مدول و زاویه فشار دایره محیطی یکسان برای هر دو چرخدنده استفاده شود.
3. برای چرخدندههای مارپیچ، همچنین لازم است که زوایای مارپیچ آنها برابر باشند، با فرض موازی بودن محورهای نصب.
نسبت تماس (ε) طول قطعه عمود مشترک بین دو چرخدنده درگیر است که توسط دایرههای سر دندانه چرخدندهها قطع میشود، تقسیم بر گام پایه (Pb) چرخدنده.
- وقتی ε <1، چرخدندهها نمیتوانند به درستی کار کنند زیرا لحظاتی وجود دارد که هیچ دندانی در تماس نیست.
- اگر 1 < ε < 2، مواقعی وجود دارد که تنها یک دندانه در تماس است. به عنوان مثال، با ε = 1.63، میتوانید بهطور میانگین 1.63 جفت دندانه درگیر را تصور کنید. در طول 37% از فرآیند انتقال، تنها یک دندانه درگیر است، در حالی که در طول 63%، دو دندانه درگیر هستند که منجر به ضربه بیشتر در حین انتقال میشود.
- اگر ε > 2، در هر زمان معین، بیش از دو جفت دندانه در تماس هستند که منجر به انتقال نرمتر میشود.
تعداد دندانهها (Z) روی چرخدندهها یک عامل مهم تأثیرگذار بر نسبت تماس است.
برای چرخدندههای کوچکتر، اغلب از چرخدندههای مارپیچی برای افزایش نسبت تماس استفاده میشود. با این حال، هزینه تولید چرخدندههای مارپیچی بهطور قابلتوجهی بیشتر از چرخدندههای ساده است.
روش دیگر استفاده از زاویه فشار کوچکتر دایره گام است، اما این تأثیر جزئی دارد.
طول عمر یک چرخدنده عمدتاً توسط سایش و شکستگی خستگی تعیین میشود. این مسائل از عوامل مختلفی مانند دقت پایین چرخدنده، لقی نامناسب، روانکاری ضعیف، گرمای بیش از حد و موارد دیگر ناشی میشوند. در حالی که محاسبه طول عمر با فرمولهای تجربی چالشبرانگیز است، دقت چرخدنده و ماده مورد استفاده عوامل حیاتی برای طول عمر آن هستند.



دیدگاهها بسته شدهاند.