Inhaltsübersicht
Umschalten aufMessung der gemeinsamen Normallänge bei Zahnradprüfverfahren
Bei der Erörterung von Prüfmethoden für Zahnräder stellt die Messung der Länge der gemeinsamen Normallinie ein einfaches und kostengünstiges Verfahren dar, das in der Getriebeproduktion und bei Prüfungen der Umkehrtechnik weit verbreitet ist.
Diese Methode vereinfacht im Vergleich zur herkömmlichen Messung der Einzelzahndicke nicht nur den Vorgang, sondern vermeidet auch wirksam Probleme im Zusammenhang mit lokalen elastischen Verformungen, die durch Punktkontakt verursacht werden, und erhöht so die Genauigkeit der Messungen. Bei der Messung der Zahndicke mit Zahnmessschiebern muss sichergestellt werden, dass die Messschieber parallel zur Zahnoberfläche bleiben, was zweifellos die Schwierigkeit der Messung erhöht. Außerdem ist die Verwendung von CNC-Maschinen (Computer Numerical Control) für die Messung zwar präzise, aber auch kostspielig und das Verfahren ist umständlich.
Dieser Artikel beginnt mit einer Einführung in das Grundkonzept der Evolventenlinie und vertieft nach und nach das Konzept der Getriebenennormale. Am Ende dieses Artikels sollten Sie ein umfassendes Verständnis davon haben und in der Lage sein, dieses Wissen bei Ihrer Arbeit effektiv anzuwenden.
Das Grundkonzept des Unbeugsamen
Einführung in Involute: Vereinfachtes Verständnis und Grundkenntnisse
Die Evolvente, ein in der Mathematik und im Ingenieurwesen häufig verwendetes Konzept, lässt sich durch ein einfaches Experiment verstehen: Stellen Sie sich vor, Sie haben einen nicht elastischen dünnen Faden um einen kreisförmigen Gegenstand gewickelt (stellen Sie sich einen perfekten Kreis vor). Wenn wir beginnen, diese Schnur langsam abzuwickeln, während wir sie straff halten, bildet der Weg, den das Ende der Schnur nimmt, eine so genannte Involute. In diesem Prozess wird das kreisförmige Objekt als “Basiskreis” und die abwickelnde Schnur als “Erzeugungslinie” bezeichnet.”

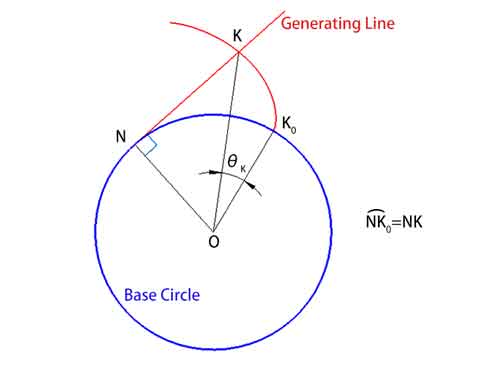
Bei dieser Aktion bleibt die erzeugende Linie tangential zum Grundkreis, und in jedem Punkt der Evolvente steht sie senkrecht zur Kurve. Dieser Winkel, den wir den Abwicklungswinkel θ (∠KOK0) nennen, ist der Winkel, den die Verbindungslinie zwischen dem Punkt auf der Evolvente (K) und dem Mittelpunkt des Grundkreises (O) vom Ausgangspunkt der Evolvente (K0) bildet.
Da sich die Länge der Schnur nicht ändert, sind die Bogenlänge auf dem Basiskreis (Bogen NK0) und die Länge der erzeugenden Linie (NK) numerisch gleich.
Das Konzept des Druckwinkels α und seine Variabilität
Betrachten wir nun ein Konzept, das eng mit der Evolvente zusammenhängt, den Druckwinkel α. Der Druckwinkel ist der Winkel zwischen der Normalen an einem beliebigen Punkt der Evolvente (d. h. der Linie senkrecht zur Evolvente) und der Richtung der Geschwindigkeit durch diesen Punkt. Es ist wichtig zu beachten, dass der Druckwinkel an jedem Punkt entlang der Evolvente variiert, wobei er am Anfang der Evolvente bei Null beginnt und nach außen hin allmählich zunimmt.
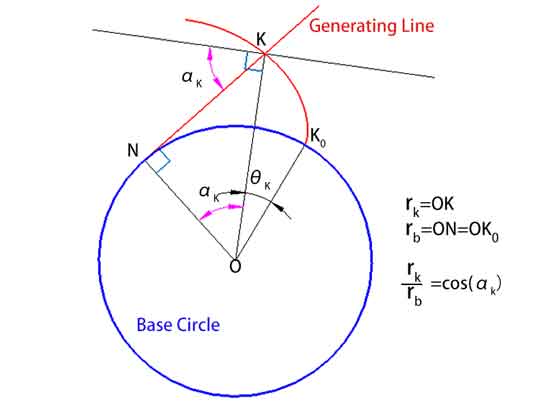
Zusätzlich kann der Abstand von einem Punkt K auf der Evolvente zum Mittelpunkt des Kreises, rk, mit der Formel rk = rb / cos(αk) berechnet werden, wobei rb der Radius des Grundkreises und αk der Eingriffswinkel im Punkt K ist.
Gemeinsame normale Funktion
Die funktionale Beziehung zwischen dem Abwicklungswinkel θ und dem Eingriffswinkel α wird als Evolventenfunktion bezeichnet, die mit inv(α) bezeichnet wird.
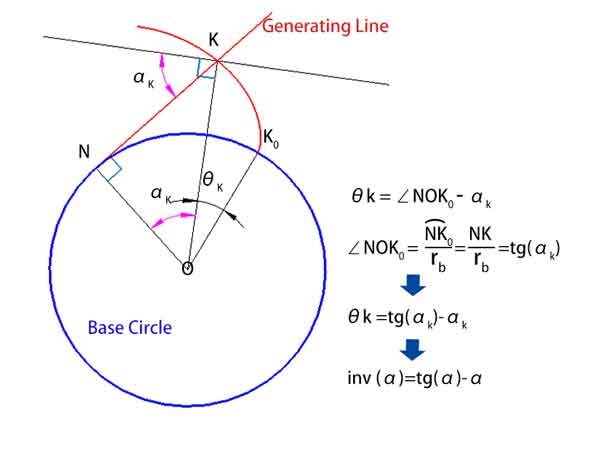
Wie im nachstehenden Diagramm dargestellt, ist θk = ∠NOK0 - αk
Dabei ist ∠NOK0 gleich derBogenlänge NK0 geteilt durch den Radius rb, gemessen in Bogenlängeneinheiten, die auch in Grad umgerechnet werden können.
Da die Bogenlänge NK0 = NK, also = NK / rb = tg(αk)
Daraus ergibt sich: θk = tg(αk) - αk
Das bedeutet inv(αk) = tg(αk) - αk
Das Konzept der gemeinsamen Norm des Fanggeräts
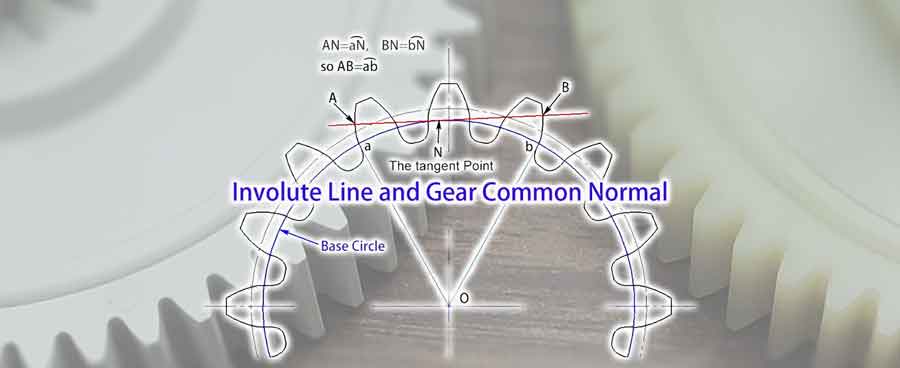
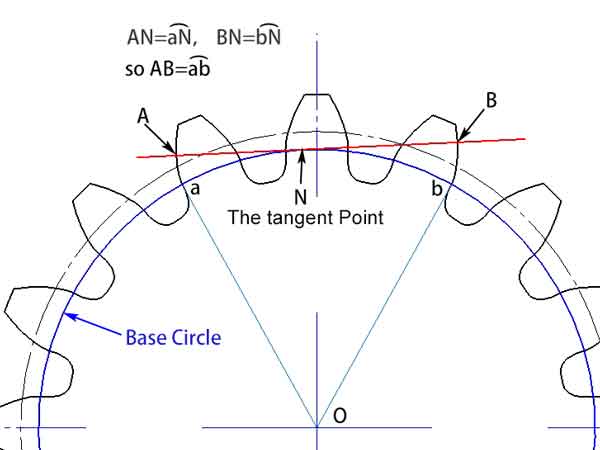
Nachdem wir das Grundkonzept der Evolvente verstanden haben, können wir uns nun mit dem Konzept der gemeinsamen Normalen des Zahnrads befassen. Sie bezieht sich auf jede Tangente auf dem Grundkreis, die die Zahnradprofile in Punkten schneidet, die durch mehrere Zähne getrennt sind. Aufgrund der Eigenschaften der Evolvente wissen wir, dass diese Linie senkrecht zu den Evolventen verläuft, die diese beiden Zahnradprofile bilden, weshalb sie auch als gemeinsame Normale bezeichnet wird.
Aus den Abbildungen geht hervor, dass die lLänge der gemeinsamen Normalen (AB), die zwischen diesen beiden Zahnradprofilen liegt, gleich der Bogenlängeab auf dem Grundkreis ist. Selbst wenn sich der Winkel der gemeinsamen Normalen ändert, bleibt ihre Länge konstant. Diese Eigenschaft bietet einen erheblichen Vorteil bei Messungen. Es bedeutet, dass selbst eine Abweichung in der Position des Messwerkzeugs keinen Einfluss auf das Ergebnis der Messung hat.
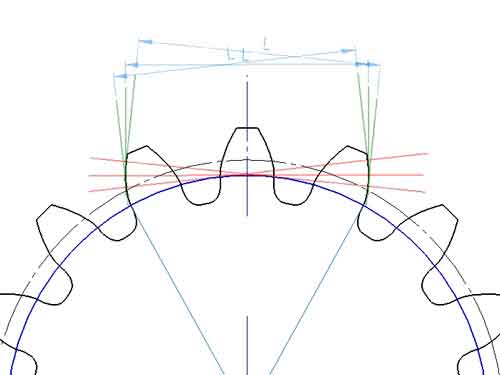
überspannte Zahnzahl
Die Anzahl der Zähne, die von der gemeinsamen Normallänge des Zahnrads aufgespannt werden, wird als “aufgespannte Zahnzahl” bezeichnet, die anhand der auf dem Bauplan eingezeichneten gemeinsamen Normale bestimmt werden kann. Es gibt eine Formel zu ihrer Berechnung, aber der Berechnungsprozess kann etwas umständlich sein, so dass die direkte Beobachtung anhand des Bauplans einfacher und unkomplizierter ist. Die Formel lautet:
k = zα / 180° + 0,5
Wo:
kist die aufgespannte Zahnzahl,zist die Anzahl der Zähne,αist der Eingriffswinkel des Zahnrads auf dem Umfangskreis, der in den meisten Fällen 20° beträgtxist das Getriebe Profilverschiebungskoeffizient.
Die Länge der gemeinsamen Normale kann auch aus CAD-Zeichnungen entnommen werden, sie kann aber auch mit einer Formel berechnet werden. Für Zahnräder mit einem Modifikationskoeffizienten x = 0 lautet die Formel zur Berechnung des Zahnabstands:
L = m cos α [(k - 0,5)π + z inv α]
Wo:
List die Länge der gemeinsamen Normale,αist der Eingriffswinkel an der Referenzkreis,kist die aufgespannte Zahnzahl.
Die oben genannten Formeln werden auf der Grundlage des Modifikationskoeffizienten x = 0 berechnet, wobei die Zahndicke am Teilkreis s = zm/2 ist, was der Hälfte der Teilung entspricht. Ist jedoch x > 0, nimmt die Zahndicke am Teilkreis zu, was zu einer Zunahme von L führt, und umgekehrt nimmt L ab, wenn x < 0. Daher ist die Messung der Länge der gemeinsamen Normale eine wirksame Methode für das Reverse Engineering von Zahnrädern, mit der sich der Modifikationskoeffizient des Musterzahnrads abschätzen lässt.
Schlussfolgerung
Um diesen Artikel kurz zu halten, werden wir hier nicht auf die Herleitung dieser Formeln eingehen, sondern sie werden in anderen Artikeln behandelt.
Wir hoffen, dass dieser Artikel Ihnen ein klares Konzept des Normalen vermittelt. Wenn Sie Fragen haben, hinterlassen Sie bitte unten Ihre Kommentare.