İçindekiler
GeçişDişli Muayene Yöntemlerinde Ortak Normal Uzunluğun Ölçülmesi
Dişli denetim yöntemleri tartışılırken, ortak normal hattın uzunluğunun ölçülmesi, dişli üretiminde ve tersine mühendislik denetimlerinde yaygın olarak kullanılan basit ve uygun maliyetli bir teknik sunar.
Bu yöntem, geleneksel bireysel diş kalınlığı ölçümüne kıyasla, sadece işlemi basitleştirmekle kalmaz, aynı zamanda noktasal temasın neden olduğu yerel elastik deformasyonla ilgili sorunları etkili bir şekilde önler, böylece ölçümlerin doğruluğunu artırır. Diş kalınlığı için dişli diş kumpasları ile ölçüm yaparken, kumpasların diş yüzeyine paralel kalmasını sağlamak çok önemlidir ve bu da şüphesiz ölçümün zorluğunu artırır. Ayrıca, ölçüm için CNC (Bilgisayarlı Nümerik Kontrol) ekipmanı kullanmak hassas olmasına rağmen, aynı zamanda maliyetlidir ve süreç zahmetlidir.
Bu makale involüt çizgisinin temel kavramını tanıtarak başlayacak ve giderek dişlinin ortak normali kavramının derinlerine inecektir.
Değişmezliğin Temel Kavramı
Involute'a Giriş: Basitleştirilmiş Anlayış ve Temel Bilgi
Matematik ve mühendislikte sıkça bahsedilen bir kavram olan involüt basit bir deneyle anlaşılabilir: dairesel bir nesnenin etrafına sarılmış elastik olmayan ince bir ipimiz olduğunu hayal edin (bunu mükemmel bir daire olarak düşünün). Bu ipi gergin tutarak yavaşça çözmeye başladığımızda, ipin ucunun izlediği yol involute olarak adlandırılan yolu oluşturur. Bu süreçte, dairesel nesne “temel daire” olarak adlandırılır ve çözülen ip “üreten çizgi” olarak bilinir.”

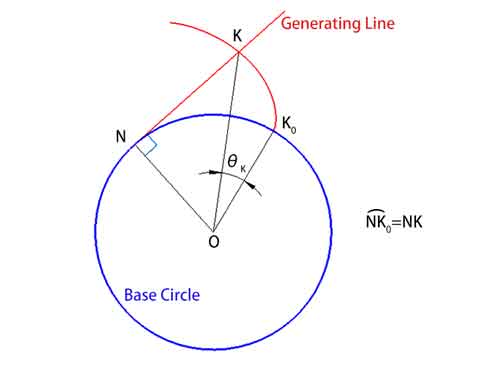
Bu eylemde, üreten doğru taban çemberine teğet kalır ve involüt üzerindeki herhangi bir noktada eğriye diktir. Sarma açısı θ (∠KOK0) olarak adlandırdığımız bu açı, (K) involütü üzerindeki noktayı (K0) başlangıç noktasından (O) taban çemberinin merkezine birleştiren doğrunun oluşturduğu açıdır.
İpin uzunluğu değişmediğinden, taban çemberindeki yay uzunluğu (NK0 yayı) ile üreten çizginin uzunluğunun (NK) sayısal olarak eşit olduğunu belirtmek gerekir.
Basınç Açısı α Kavramı ve Değişkenliği
Daha derine inerek, involütle yakından ilgili bir kavramı tartışalım - basınç açısı α. Basınç açısı, involüt üzerindeki herhangi bir noktadaki normal (yani involüte dik doğru) ile o noktadan geçen hız yönü arasındaki açıdır. Basınç açısının involüt boyunca her noktada değiştiğini, involüt başlangıcında sıfırdan başladığını ve dışarı doğru hareket ettikçe kademeli olarak arttığını belirtmek önemlidir.
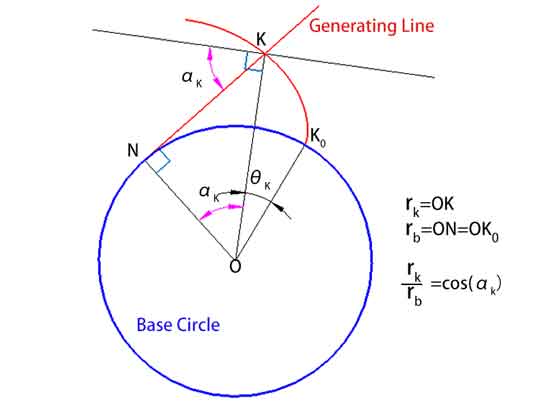
Ayrıca, involüt üzerindeki bir K noktasından dairenin merkezine olan mesafe, rk, rk = rb / cos(αk) formülü kullanılarak hesaplanabilir; burada rb temel dairenin yarıçapı ve αk K noktasındaki basınç açısıdır.
Yaygın Normal İşlev
Çözülme açısı θ ile basınç açısı α arasındaki fonksiyonel ilişki, inv(α) ile gösterilen involüt fonksiyonu olarak adlandırılır.
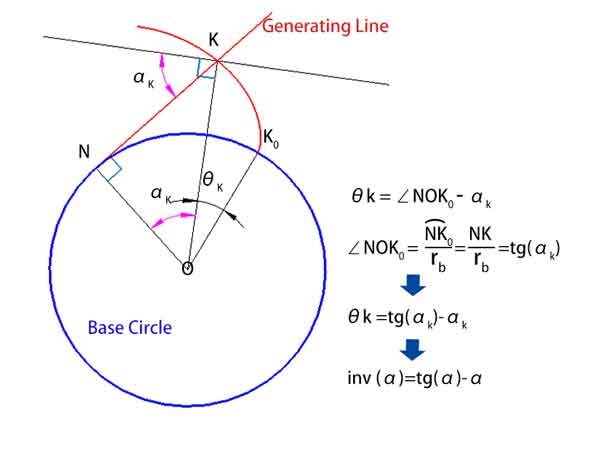
Aşağıdaki diyagramda gösterildiği gibi, θk = ∠NOK0 - αk
Burada, ∠NOK0, yay uzunluğu NK0'nin rb yarıçapına bölünmesine eşittir ve yay uzunluğu birimleriyle ölçülür, bu da dereceye dönüştürülebilir.
Yay uzunluğu NK0 = NK olduğundan, = NK / rb = tg(αk)
Böylece, θk = tg(αk) - αk
Bu da inv(αk) = tg(αk) - αk anlamına gelir.
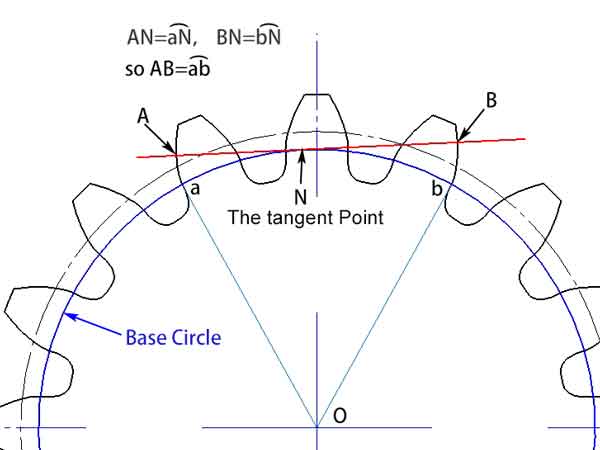
Dişlinin Ortak Normali Kavramı
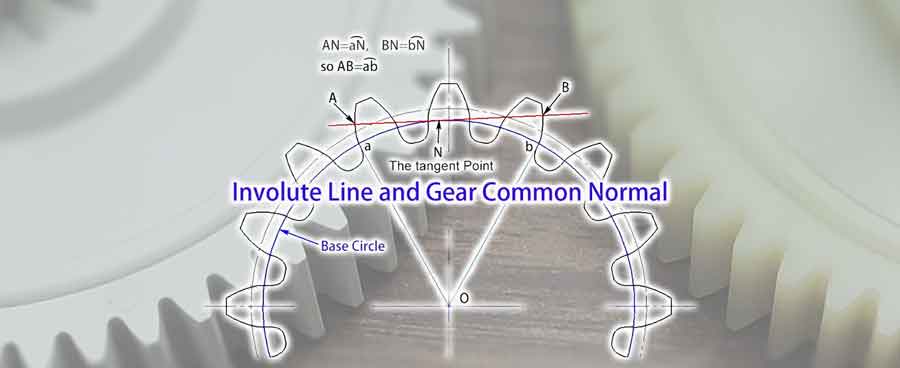
Temel involüt kavramını anladıktan sonra, artık dişlinin ortak normali kavramını inceleyebiliriz. Bu, dişli profillerini birkaç dişle ayrılan noktalarda kesen temel daire üzerindeki herhangi bir teğet çizgiyi ifade eder. Tutulumun özelliklerinden dolayı, bu çizginin bu iki dişli profilini oluşturan tutulumlara dik olduğunu biliyoruz, bu yüzden ortak normal olarak adlandırılır.
Çizimlerden, bu iki dişli profili arasında yer alan (AB) ortak normalin luzunluğunun, taban dairesi üzerindeki yay uzunluğunaab eşit olduğunu gözlemleyebiliriz. Ortak normalin açısı değişse bile uzunluğu sabit kalır. Bu özellik ölçümlerde önemli bir avantaj sağlar. Ölçüm aletinin konumunda bir miktar sapma olsa bile, ölçümün sonucunu etkilemeyeceği anlamına gelir.
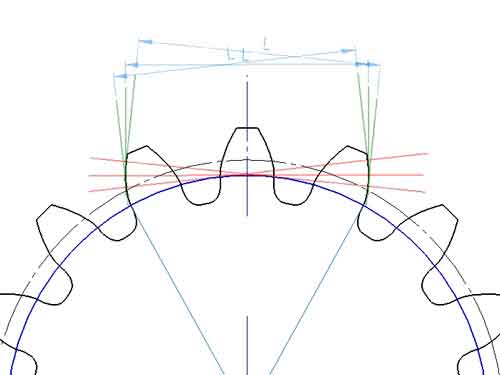
yayılmış diş numarası
Dişli ortak normal uzunluğu tarafından yayılan diş sayısına “yayılan diş sayısı” denir ve bu sayı plan üzerinde çizilen ortak normalden belirlenebilir. Bunu hesaplamak için bir formül vardır, ancak hesaplama süreci biraz zahmetli olabilir, bu nedenle plan üzerinden doğrudan gözlem yapmak daha basit ve anlaşılırdır. Formül şöyledir:
k = zα / 180° + 0,5
Nerede?
kyayılmış diş sayısıdır,zdiş sayısıdır,αdişlinin çevre çemberi üzerindeki basınç açısıdır ve çoğu durumda 20°'dirxdişli profil kaydırma katsayısı.
Ortak normalin uzunluğu CAD çizimlerinden de elde edilebilir, ancak bir formül kullanılarak da hesaplanabilir. Modifikasyon katsayısı x = 0 olan dişliler için, yayılmış diş mesafesini hesaplama formülü şöyledir:
L = m cos α [(k - 0.5)π + z inv α]
Nerede?
Lortak normalin uzunluğudur,α'deki basınç açısıdır. referans çemberi,kyayılmış diş sayısıdır.
Yukarıda belirtilen formüller, hatve dairesindeki diş kalınlığının hatvenin yarısı olan s = zm/2 olduğu x = 0 modifikasyon katsayısına göre hesaplanır. Bununla birlikte, x > 0 ise, hatve dairesindeki diş kalınlığı artar ve L'de bir artışa neden olur ve tersine, x < 0 ise L azalır. Bu nedenle, ortak normalin uzunluğunun ölçülmesi, dişli tersine mühendisliği için etkili bir yöntemdir ve örnek dişlinin modifikasyon katsayısının tahmin edilmesini sağlar.
Sonuç
Bu makaleyi kısa tutmak için, bu formüllerin türetilmesine burada girmeyeceğiz, ancak diğer makalelerde ele alınacaktır.
Umarız bu makale size genel normal hakkında net bir fikir verir. Herhangi bir sorunuz varsa, lütfen yorumlarınızı aşağıya bırakın.