Índice
AlternarEsta é uma versão mais simples da terminologia das engrenagens e das fórmulas de cálculo dos dentes
Esta publicação tem como objetivo explicar a terminologia das engrenagens e as fórmulas de cálculo dos dentes de uma forma mais fácil para os principiantes e também para aqueles que já aprenderam engrenagens há muito tempo, mas que pretendem retomá-las rapidamente.
As engrenagens têm muitos parâmetros que exigem um pouco de matemática e treinamento geométrico para entendê-los completamente. No entanto, não é necessário aprofundar muito os conceitos básicos do conhecimento de engrenagens, depois de ler este post, você deve ser capaz de fazer projetos preliminares de engrenagens ou ter uma comunicação eficaz com designers de engrenagens.
Comecemos pela forma básica de engrenagem, as engrenagens rectas:
Índice de conteúdo
1. Número de dentes (z); 2. Círculo de referência e diâmetro de referência (d); 3. Módulo (m); 4. Distância do centro (a); 5.Ângulo de pressão (α); 6.Número mínimo de dentes (zmin); 7.Coeficiente de deslocamento do perfil (x); 8. Tabela de resumo.
1. Número de dentes (z)
É bastante simples: é o número de dentes da engrenagem.
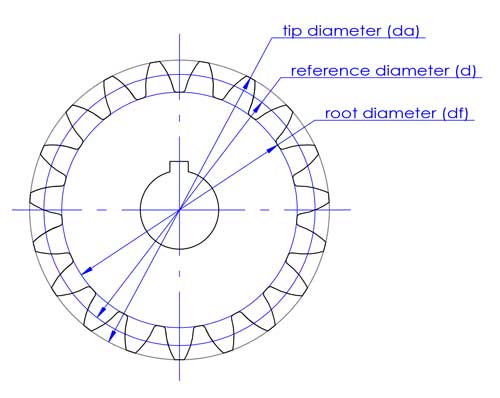
2. Círculo de referência e diâmetro de referência (d)
O diâmetro da ponta (da) e o diâmetro da raiz (df) correspondem à parte superior e inferior dos dentes.
O diâmetro de referência é utilizado na conceção e cálculo de engrenagens. Está diretamente relacionado com outros parâmetros importantes da engrenagem, como o módulo (m), a distância entre centros (c) e o ângulo de pressão (α).
O diâmetro da ponta (da) e o diâmetro da raiz (df) correspondem à parte superior e inferior dos dentes.
O diâmetro de referência é utilizado na conceção e cálculo de engrenagens. Está diretamente relacionado com outros parâmetros importantes da engrenagem, como o módulo (m), a distância entre centros (c) e o ângulo de pressão (α).
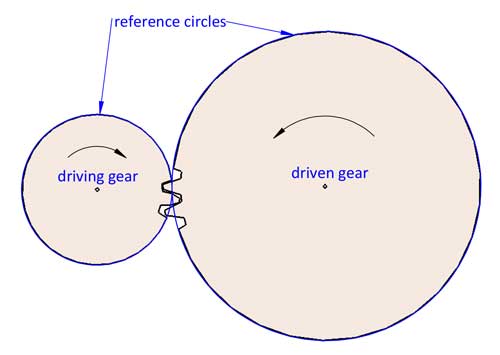
A rotação de 2 engrenagens pode ser considerada como a rotação engatada de 2 círculos de referência sem deslizamento. A relação de transmissão i=d2/d1. d1 e d2 referem-se aos diâmetros de referência de 2 engrenagens acopladas (a engrenagem 1 é a engrenagem motriz e a engrenagem 2 é a engrenagem movida).

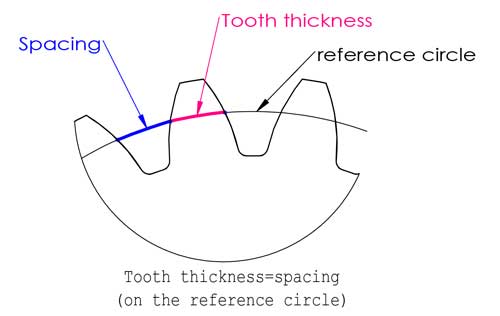
O círculo de referência está localizado algures entre a ponta e a base dos dentes, normalmente é onde a espessura do dente é igual ao espaçamento, mas nem sempre é o caso (falaremos sobre a mudança de perfil mais tarde neste post).
3. Módulo (m)
O módulo é provavelmente o parâmetro mais importante da engrenagem e aparece quase sempre nas fórmulas de cálculo dos dentes. Na verdade, não é tão difícil de compreender como se poderia imaginar. Primeiro, vamos perceber o que é o passo. O passo é o comprimento do arco entre pontos correspondentes em dentes adjacentes, normalmente no círculo de referência.
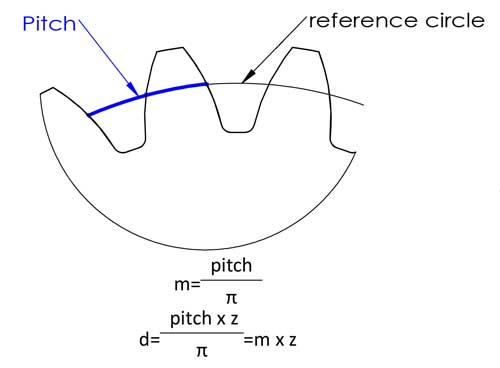

Então temos o diâmetro de referência d=circunferência/π=pitch*z/π, para facilitar o cálculo, definimos o pitch/π como o módulo, e agora temos a equação de d=m*z, isso facilita muito o cálculo, certo? Os módulos foram padronizados nos seguintes números (unidade: mm):
Primeira série (recomendada): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Segunda série (menos utilizada): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
No entanto, para as engrenagens de plástico moldado por injeção, não é necessário adotar estes números de módulo padrão, uma vez que os dentes não são cortados por cortadores de dentes padrão.
Agora temos a relação de transmissão i=d2/d1=z2/z1 (a engrenagem 1 é a engrenagem motora e a engrenagem 2 é a engrenagem movida).
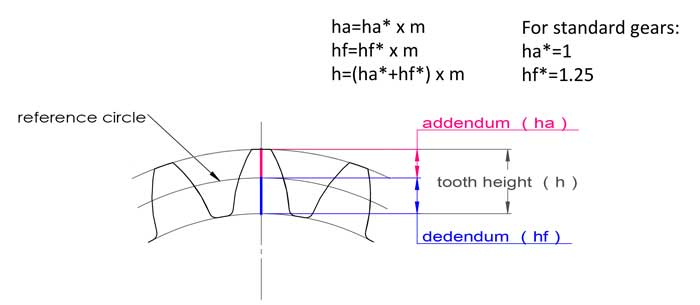
O módulo também tem a ver com a altura do dente, para engrenagens padrão, a altura do dente é igual a 2,25*m:
addendum ha=1*m, dedendum hf=1,25*m, altura do dente h=2,25*m.
4. Distância ao centro (a)
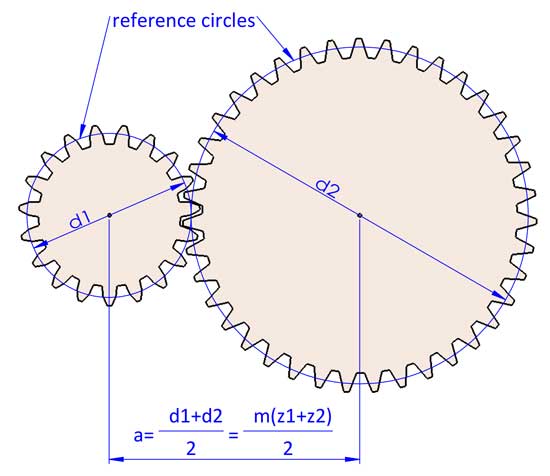
2 engrenagens têm sempre o mesmo módulo, caso contrário não coincidem. Agora podemos concluir que a=(d1+d2)/2=m(z1+z2)/2, mas pode ser ligeiramente diferente se fizermos alguns ajustes nas geometrias das engrenagens (mudança de perfil dos dentes).
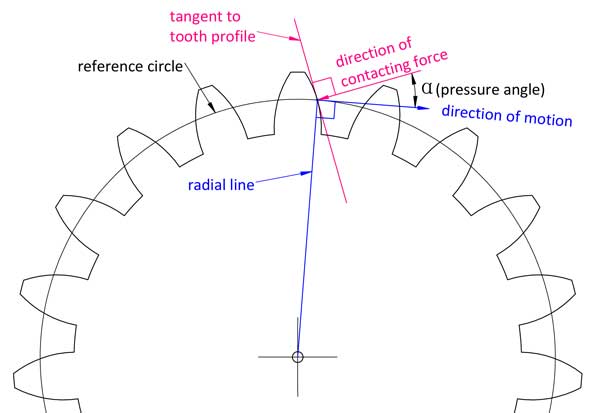
Simplificando, como o seu nome sugere, é o ângulo entre a direção da força de contacto no ponto de contacto do dente e a direção do movimento desse ponto no perfil do dente.
Em geometria, é o ângulo entre a reta normal ao perfil do dente involuto e a reta normal à sua linha radial.
Se quiser entender completamente o ângulo de pressão, então precisa de ir mais fundo para entender a linha involuta do perfil do dente. Esta é apenas uma forma mais fácil de explicação.
Diferentes pontos no perfil do dente têm diferentes ângulos de pressão, mas quando falamos do ângulo de pressão de uma engrenagem, refere-se normalmente ao do círculo de referência. A maioria das engrenagens utiliza 20° como ângulo de pressão, algumas têm 14,5° ou 25°. 2 engrenagens de encaixe devem ter o mesmo módulo e ângulo de pressão.
6. Número mínimo de dentes (zmin) sem que a engrenagem seja reduzida
Não se pode ter qualquer número de dentes da engrenagem que se queira. Se houver muito poucos dentes, a parte inferior dos dentes estará abaixo do ponto limite, como consequência, quando os dentes são feitos por cortadores de dentes, uma parte em excesso da raiz dos dentes será cortada.
7. Coeficiente de deslocação do perfil (x)
Normalmente, para o perfil do dente, a adenda dos dentes ha=1*m, e a dedenda hf=1,25*m, no entanto, o perfil dos dentes pode ser deslocado um pouco para cima ou para baixo:
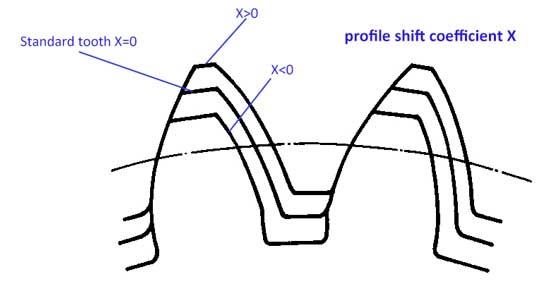

Agora temos o coeficiente de deslocação do perfil (x). Quando o perfil é deslocado para cima, o valor de x é positivo (x>0), e se o perfil é deslocado para baixo, o valor de x é negativo (x<0).
Com o movimento do perfil dos dentes, agora temos:
- adenda ha=(1+x)*m
- dedendum hf=(1,25-x)*m
A altura do dente h=ha+hf=2,25*m, continua a ser a mesma dos dentes normais.
As principais razões para a mudança de perfil são:
1) Com o perfil deslocado, podemos evitar o corte inferior dos dentes com um menor número de dentes. A fórmula é a seguinte:
xmin=(17-z)/17
Por exemplo, se quiser que o número de dentes seja 14, então X=(17-14)/17=0,176
2)Afinação fina da distância central
a=[(m+x1)z1+(m+x2)z2]/2, pelo que a distância ao centro não tem de ser (z1+z2)*m
3) Tornar o pinhão mais forte. Normalmente, o pinhão falha antes da engrenagem, ao adicionar uma mudança de perfil positivo, a parte inferior do pinhão torna-se mais larga (enquanto a ponta se torna mais estreita), tornando-o assim mais forte.
Em resumo:
| # | Artigo | Símbolo | Fórmula |
|---|---|---|---|
| 1 | número de dentes | z | |
| 2 | módulo | m | m=pitch/π |
| 3 | relação de transmissão | i | i=d2/d1=z2/z1 1: engrenagem motriz, e 2: engrenagem movida |
| 4 | coeficiente de adenda | da* | da*=1+x x=0 para engrenagens standard |
| 5 | coeficiente dedendum | df* | df*=1,25-x |
| 6 | coeficiente de deslocação do perfil | x | Para engrenagens standard,, x=0 |
| 7 | ângulo de pressão | α | α=20° para a maioria das engrenagens Outros menos utilizados são 14,5° e 25°. |
| 8 | diâmetro de referência | d | d=mz |
| 9 | diâmetro da ponta | da | da=d+2Ha* x m, da=(z+2ha*) m Para engrenagens normais, da=(z+2) x m |
| 10 | diâmetro da raiz | df | df=d-2Hf* x m, df=(z-2hf*) x m Para engrenagens standard, df=(z-2,5) x m |
| 11 | adenda | ha | ha=m x ha* Para engrenagens standard, ha=m |
| 12 | dedendum | hf | hf=m x hf* Para engrenagens standard, hf=1,25m |
| 13 | altura do dente | h | h=m x (ha*+hf*) ha*+Hf*=2,25 para a maioria das mudanças |
| 14 | distância do centro | a | a=m x (z1+z2)/2 para engrenagens standard a=[(m+x1)z1+(m+x2)z2]/2 para engrenagens com mudança de perfil |
| 15 | Número mínimo de dentes sem rebaixamento | Zmin | Zmin=2ha*/sinα^2 Zmin=17 quando ha*=1, α=20° |
| 16 | Deslocação mínima do perfil sem subcotação | Xmin | Xmin=(17-z)/17 |
Perguntas mais frequentes
Introdução às forças de engrenagem
No processo de engrenamento entre duas engrenagens, a força exercida pela engrenagem motriz sobre a engrenagem movida pode ser decomposta numa força normal perpendicular à superfície da engrenagem movida e numa força tangencial perpendicular à força normal. A força tangencial não participa no acionamento da engrenagem motriz e provoca o desgaste entre as duas engrenagens. O ângulo no ponto de engrenamento das engrenagens motora e movida é maior no início e no fim do engate e menor no meio. Quando o ponto de engrenamento está na linha central das duas engrenagens, é igual a zero. Por conseguinte, um ângulo mais pequeno pode melhorar a eficiência da transmissão e reduzir o desgaste.
Relação entre o ângulo de pressão e o ângulo da malha
O ângulo de pressão está diretamente relacionado com o ângulo de engrenamento. Por outro lado, um ângulo de pressão menor resulta em raízes de engrenagens mais finas, o que reduz a resistência das engrenagens. Por conseguinte, é importante encontrar um equilíbrio.
Normas industriais para ângulos de pressão de engrenagens
- Na produção industrial atual, a maioria das engrenagens standard utiliza um ângulo de pressão de 20°.
- As engrenagens concebidas para cargas leves e velocidades elevadas utilizam frequentemente um ângulo de pressão de 14,5°, que tem as vantagens de um menor ruído e de uma maior eficiência de transmissão.
- As engrenagens concebidas para aplicações de baixa velocidade e de carga pesada utilizam um ângulo de pressão de 25°, que oferece uma maior resistência dos dentes, mas à custa de uma menor eficiência de transmissão e de um maior ruído.
Engrenagens de plástico
Para as engrenagens de plástico, pode ser escolhido qualquer ângulo de pressão, uma vez que não são necessárias ferramentas de corte padrão para o seu fabrico. No entanto, para simplificar o design, é comum manter estes valores padrão.
O círculo de circunferência é a base para os cálculos de engrenagens. O seu diâmetro é calculado como o módulo (m) multiplicado pelo número de dentes (Z). Essencialmente, é um círculo teórico usado principalmente para cálculos, com outros parâmetros de engrenagem derivados dele.
O diâmetro do passo, por outro lado, é definido durante o engrenamento efetivo de duas engrenagens. É o círculo formado pela intersecção da normal comum das engrenagens e da reta que une os seus centros, passando pelo ponto de tangência. Os círculos de passo de duas engrenagens engrenadas são tangentes um ao outro. No entanto, as circunferências podem nem sempre ser tangentes
Em modelos de engrenagens padrão, o círculo de circunferência e o círculo de passo normalmente se sobrepõem. No entanto, se a distância entre centros for ajustada para aumentar a folga ou se as engrenagens tiverem sido modificadas, o círculo de circunferência e o círculo de passo podem ser diferentes.
Sim. Nos modelos padrão, a espessura do dente e a largura da ranhura no círculo de circunferência são iguais.
No entanto, em aplicações práticas, para permitir alguma folga enquanto se mantém a distância central padrão, a espessura do dente é ligeiramente mais fina.
Um método consiste em tornar a espessura do dente ligeiramente mais pequena do que a largura da ranhura no círculo de circunferência.
Um outro método consiste em instalar as engrenagens a uma distância entre centros ligeiramente superior à norma.
O tamanho necessário da folga depende da precisão de fabrico das engrenagens; uma maior precisão reduz a necessidade de folga.
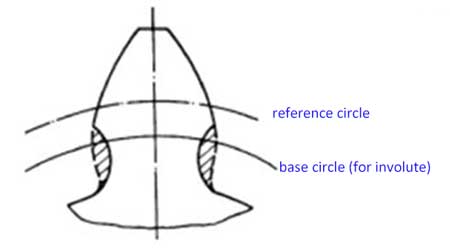
O círculo base de uma engrenagem é o círculo a partir do qual é gerado o seu involuto. O seu passo é o comprimento de arco entre pontos idênticos dos perfis de dois dentes adjacentes no círculo base, ou seja
Pb = Db/Z.
Aqui, Db é o diâmetro do círculo de base.
Ou Pb = Df * cos(α) / Z = mπ * cos(α),
em que Df é o diâmetro do círculo de circunferência, m é o módulo da engrenagem e α é o ângulo de pressão do círculo de circunferência.
1. Nas engrenagens de dentes rectos, é necessário que o engrenamento de um par de dentes esteja sincronizado com o engrenamento do par anterior. Isto exige que os seus passos de círculo de base sejam iguais, ou seja:
m1 * cos(α1) = m2 * cos(α2).
Daqui se pode deduzir que os módulos (m) de um par de engrenagens não têm necessariamente de ser iguais.
2. Ao mesmo tempo, o grau de envolvimento (relação de contacto ε) é superior a 1
Para engrenagens fabricadas com ferramentas de corte padrão, devido à padronização e serialização das ferramentas, é prática comum usar o mesmo módulo e ângulo de pressão do círculo de circunferência para ambas as engrenagens.
3. Para as engrenagens helicoidais, é igualmente necessário que os seus ângulos de hélice sejam iguais, partindo do princípio que os seus eixos de instalação são paralelos.
A relação de contacto (ε) é o comprimento do segmento normal comum entre duas engrenagens, que é cortado pelos círculos adendos das engrenagens, dividido pelo passo de base (Pb) da engrenagem.
- Quando ε <1, as engrenagens não podem funcionar corretamente porque há momentos em que nenhum dente está em contacto.
- Se 1 < ε < 2, há momentos em que apenas um dente está em contacto. Por exemplo, com ε = 1,63, pode-se imaginar uma média de 1,63 pares de dentes em contacto. Durante 37% do processo de transmissão, apenas um dente está em contacto, enquanto que durante 63%, dois dentes estão em contacto, levando a um maior impacto durante a transmissão.
- Se ε > 2, em qualquer momento, mais de dois pares de dentes estão em contacto, o que resulta numa transmissão mais suave.
O número de dentes (Z) nas engrenagens é um fator importante que afecta a relação de contacto.
Para engrenagens mais pequenas, as engrenagens helicoidais são frequentemente utilizadas para aumentar a relação de contacto. No entanto, o custo de fabrico das engrenagens helicoidais é significativamente mais elevado do que o das engrenagens de dentes rectos.
Outro método consiste em utilizar um ângulo de pressão mais pequeno do círculo de inclinação, mas este tem um efeito menor.
A vida útil de uma engrenagem é determinada principalmente pelo desgaste e pela fratura por fadiga. Estes problemas resultam de vários factores, como a baixa precisão da engrenagem, folga inadequada, lubrificação deficiente, sobreaquecimento, entre outros. Embora seja difícil calcular a vida útil com fórmulas empíricas, a precisão da engrenagem e o material utilizado são factores críticos para a sua longevidade.



Os comentários estão fechados.