Indice dei contenuti
ToggleMisura della lunghezza normale comune nei metodi di ispezione degli ingranaggi
Quando si parla di metodi di ispezione degli ingranaggi, la misurazione della lunghezza della linea normale comune rappresenta una tecnica semplice ed economica ampiamente utilizzata nella produzione di ingranaggi e nelle ispezioni di ingegneria inversa. .
Questo metodo, rispetto alla tradizionale misurazione dello spessore del singolo dente, non solo semplifica l'operazione, ma evita efficacemente i problemi legati alla deformazione elastica locale causata dal contatto puntuale, migliorando così l'accuratezza delle misure. Quando si misura lo spessore di un dente con i calibri a corsoio, è essenziale assicurarsi che i calibri rimangano paralleli alla superficie del dente, il che aumenta indubbiamente la difficoltà della misurazione. Inoltre, sebbene l'utilizzo di apparecchiature CNC (Computer Numerical Control) per la misurazione sia preciso, è anche costoso e il processo è macchinoso.
Questo articolo inizierà introducendo il concetto di base della linea di involuzione, approfondendo gradualmente il concetto di normale comune dell'ingranaggio. Alla fine di questo articolo, dovreste averne una comprensione completa ed essere in grado di applicare efficacemente queste conoscenze nel vostro lavoro.
Il concetto di base di Involuto
Introduzione a Involute: comprensione semplificata e conoscenze di base
L'involuto, un concetto spesso citato in matematica e ingegneria, può essere compreso attraverso un semplice esperimento: immaginiamo di avere una corda sottile non elastica avvolta intorno a un oggetto circolare (pensiamo a un cerchio perfetto). Quando iniziamo a srotolare lentamente questa corda mantenendola tesa, il percorso che l'estremità della corda compie forma quello che viene chiamato un involuto. In questo processo, l'oggetto circolare viene chiamato “cerchio base” e la stringa che si srotola viene chiamata “linea generatrice”.”

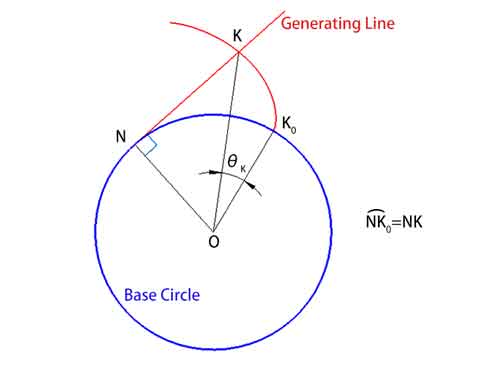
In questa azione, la linea generatrice rimane tangente al cerchio di base e in qualsiasi punto dell'involucro è perpendicolare alla curva. Questo angolo, che chiamiamo angolo di srotolamento θ (∠KOK0), è l'angolo formato dalla linea che collega il punto dell'involuta (K) al centro del cerchio di base (O) dal punto di partenza dell'involuta (K0).
Si noti che, poiché la lunghezza della corda non cambia, la lunghezza dell'arco sul cerchio di base (arco NK0) e la lunghezza della linea generatrice (NK) sono numericamente uguali.
Il concetto di angolo di pressione α e la sua variabilità
Approfondiamo un concetto strettamente legato all'involucro: l'angolo di pressione α. L'angolo di pressione è l'angolo tra la normale a un punto qualsiasi dell'involucro (cioè la linea perpendicolare all'involucro) e la direzione della velocità attraverso quel punto. È importante notare che l'angolo di pressione varia in ogni punto dell'involucro, partendo da zero all'inizio dell'involucro e aumentando gradualmente man mano che si procede verso l'esterno.
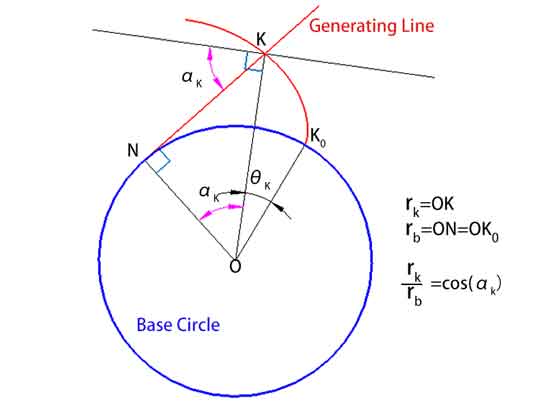
Inoltre, la distanza da un punto K dell'involucro al centro del cerchio, rk, può essere calcolata con la formula rk = rb / cos(αk), dove rb è il raggio del cerchio di base e αk è l'angolo di pressione al punto K.
Funzione normale comune
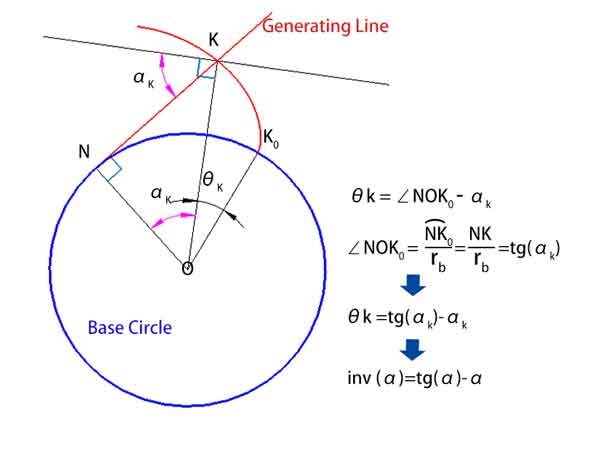
La relazione funzionale tra l'angolo di srotolamento θ e l'angolo di pressione α è denominata funzione di involuzione, indicata con inv(α).
Come mostrato nel diagramma seguente, θk = ∠NOK0 - αk
Dove il ∠NOK0 è uguale alla lunghezza dell'arco NK0 divisa per il raggio rb, misurato in unità di lunghezza d'arco, che può anche essere convertito in gradi.
Poiché la lunghezza dell'arco NK0 = NK, quindi = NK / rb = tg(αk)
Si ha quindi θk = tg(αk) - αk
Il che significa inv(αk) = tg(αk) - αk
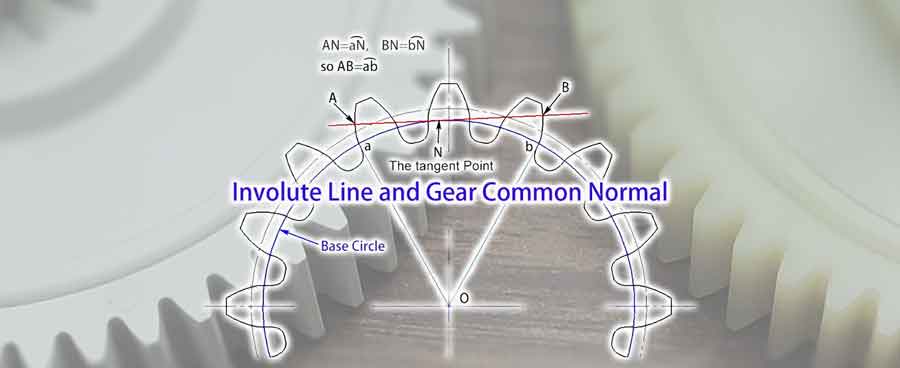
Il concetto di normalità comune dell'ingranaggio
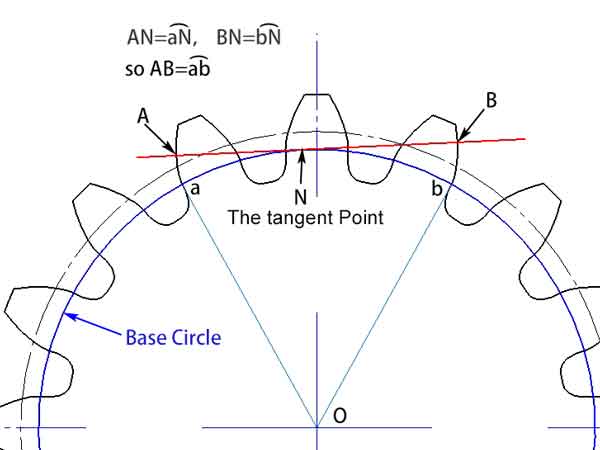
Dopo aver compreso il concetto di base dell'involucro, possiamo ora approfondire il concetto di normale comune dell'ingranaggio. Si tratta di una qualsiasi rettatangente al cerchio di base che interseca i profili dell'ingranaggio in punti separati da più denti. Grazie alle caratteristiche dell'involucro, sappiamo che questa retta è perpendicolare agli involucri che formano questi due profili di ingranaggi, per cui viene chiamata normale comune.
Dalle illustrazioni, possiamo osservare che la llunghezza della normale comune (AB), incastonata tra questi due profili di ingranaggi, è uguale alla lunghezza dell'arcoab sul cerchio di base. Anche se l'angolo della normale comune cambia, la sua lunghezza rimane costante. Questa caratteristica offre un vantaggio significativo nelle misurazioni. Significa che anche se c'è una deviazione nella posizione dello strumento di misura, questa non influisce sul risultato della misurazione.
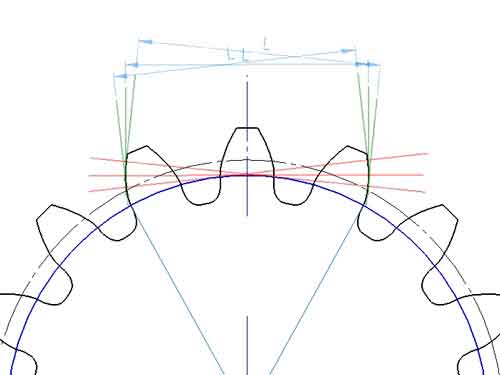
numero del dente spaziato
Il numero di denti compresi nella lunghezza della normale comune dell'ingranaggio è chiamato “numero di denti compresi”, che può essere determinato dalla normale comune disegnata sulla cianografia. Esiste una formula per calcolarlo, ma il processo di calcolo può essere piuttosto macchinoso, rendendo più semplice e diretta l'osservazione diretta dalla cianografia. La formula è:
k = zα / 180° + 0,5
Dove:
kè il numero del dente spaziato,zè il numero di denti,αè l'angolo di pressione dell'ingranaggio sulla circonferenza, che nella maggior parte dei casi è di 20°.xè l'ingranaggio coefficiente di spostamento del profilo.
La lunghezza della normale comune può essere ottenuta anche da disegni CAD, ma può anche essere calcolata con una formula. Per gli ingranaggi con un coefficiente di modifica x = 0, la formula per calcolare la distanza tra i denti è:
L = m cos α [(k - 0,5)π + z inv α]
Dove:
Lè la lunghezza della normale comune,αè l'angolo di pressione al cerchio di riferimento,kè il numero del dente spaziato.
Le formule di cui sopra sono calcolate sulla base del coefficiente di modifica x = 0, dove lo spessore del dente sul cerchio del passo s = zm/2, che è la metà del passo. Tuttavia, se x > 0, lo spessore del dente sul cerchio del passo aumenta, portando a un aumento di L, e viceversa, L diminuisce se x < 0. Pertanto, la misurazione della lunghezza della normale comune è un metodo efficace per il reverse engineering degli ingranaggi, che consente di stimare il coefficiente di modifica dell'ingranaggio campione.
Conclusione
Per mantenere l'articolo conciso, non ci addentreremo nella derivazione di queste formule, che verranno trattate in altri articoli.
Ci auguriamo che questo articolo vi fornisca un concetto chiaro della normalità comune. Se avete domande, lasciate pure i vostri commenti qui sotto.