Indice dei contenuti
ToggleQuesta è una versione più semplice della terminologia degli ingranaggi e delle formule di calcolo dei denti.
Questo post ha lo scopo di spiegare la terminologia degli ingranaggi e le formule di calcolo dei denti in modo più semplice per i principianti e anche per coloro che hanno imparato gli ingranaggi molto tempo fa ma vogliono riprenderli rapidamente.
Gli ingranaggi hanno molti parametri che richiedono un po' di matematica e di formazione geometrica per essere compresi appieno. Tuttavia, non è necessario approfondire troppo i concetti di base della conoscenza degli ingranaggi; dopo aver letto questo post, dovreste essere in grado di realizzare progetti preliminari di ingranaggi o di comunicare efficacemente con i progettisti di ingranaggi.
Partiamo dalla forma di ingranaggio di base, gli ingranaggi cilindrici:
Tabella dei contenuti
1. Numero di denti (z); 2. Cerchio di riferimento e diametro di riferimento (d) Cerchio di riferimento e diametro di riferimento (d); 3. Modulo (m); 4. Distanza dal centro (a). Distanza dal centro (a); 5. Angolo di pressione (α); 6. Angolo di pressione (α).Numero minimo di denti (zmin); 7.Coefficiente di spostamento del profilo (x); 8. Tabella riassuntiva.
1. Numero di denti (z)
Si tratta del numero di denti dell'ingranaggio.
2. Cerchio di riferimento e diametro di riferimento (d)
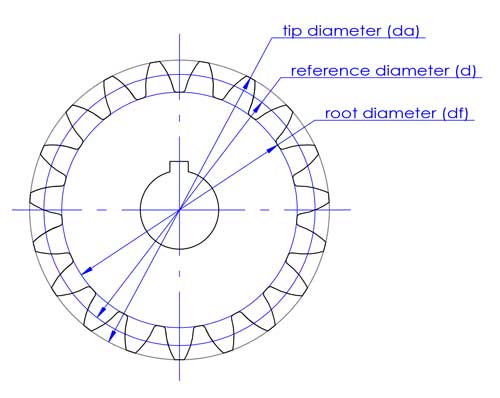
Il diametro della punta (da) e il diametro della radice (df) corrispondono alla parte superiore e inferiore dei denti.
Il diametro di riferimento viene utilizzato nella progettazione e nel calcolo degli ingranaggi. È direttamente collegato ad altri importanti parametri degli ingranaggi, come il modulo (m), l'interasse (c) e l'angolo di pressione (α).
Il diametro della punta (da) e il diametro della radice (df) corrispondono alla parte superiore e inferiore dei denti.
Il diametro di riferimento viene utilizzato nella progettazione e nel calcolo degli ingranaggi. È direttamente collegato ad altri importanti parametri degli ingranaggi, come il modulo (m), l'interasse (c) e l'angolo di pressione (α).
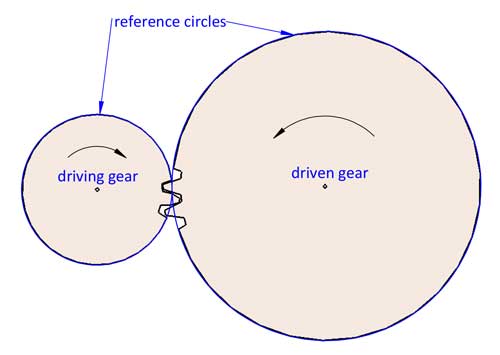
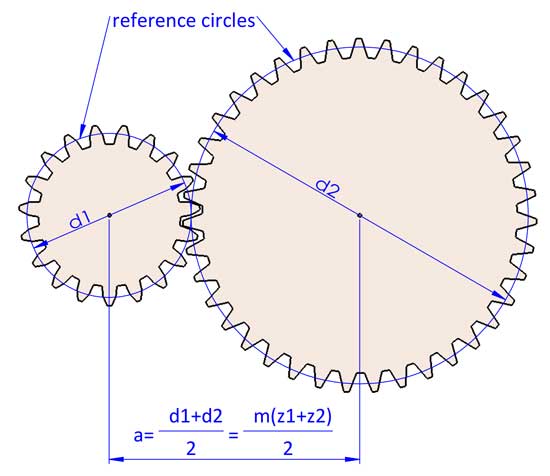
La rotazione di 2 ingranaggi può essere considerata come una rotazione impegnata di 2 cerchi di riferimento senza slittamento. Il rapporto di trasmissione i=d2/d1. d1 e d2 si riferiscono ai diametri di riferimento dei 2 ingranaggi accoppiati (l'ingranaggio 1 è l'ingranaggio motore e l'ingranaggio 2 è l'ingranaggio condotto).

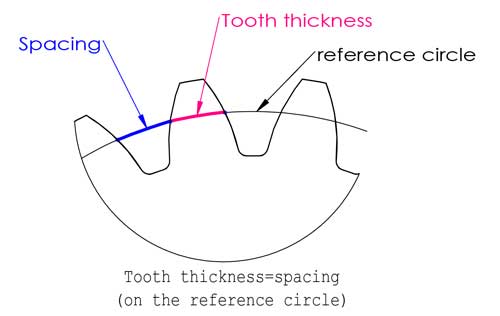
Il cerchio di riferimento si trova da qualche parte tra la punta e la base dei denti, di solito è dove lo spessore del dente è uguale alla distanza, ma non è sempre così (parleremo dello spostamento del profilo più avanti in questo post).
3. Modulo (m)
Il modulo è probabilmente il parametro più importante degli ingranaggi e compare quasi ovunque nelle formule di calcolo dei denti. In realtà, non è così difficile da capire come si potrebbe immaginare. Prima di tutto cerchiamo di capire cos'è il passo: il passo è la lunghezza dell'arco tra punti corrispondenti su denti adiacenti, di solito sul cerchio di riferimento.
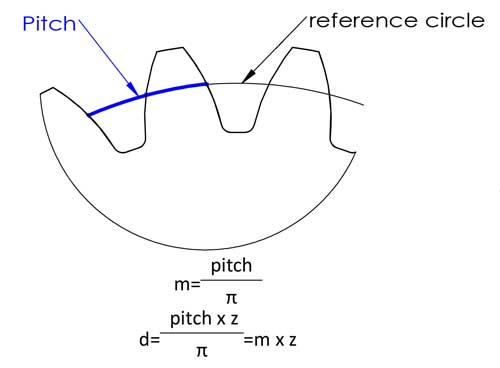

Poi abbiamo il diametro di riferimento d=circonferenza/π=pitch*z/π, per facilitare il calcolo, definiamo il pitch/π come modulo, e ora abbiamo l'equazione di d=m*z, questo rende il calcolo molto più facile, giusto? I moduli sono stati standardizzati nei seguenti numeri (unità: mm):
Prima serie (raccomandata): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Seconda serie (meno utilizzata): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Tuttavia, per gli ingranaggi in plastica stampati a iniezione non è necessario adottare questi numeri di modulo standard, poiché i denti non vengono tagliati da frese standard.
Ora abbiamo il rapporto di trasmissione i=d2/d1=z2/z1 (la marcia 1 è la marcia motrice e la marcia 2 è la marcia condotta).
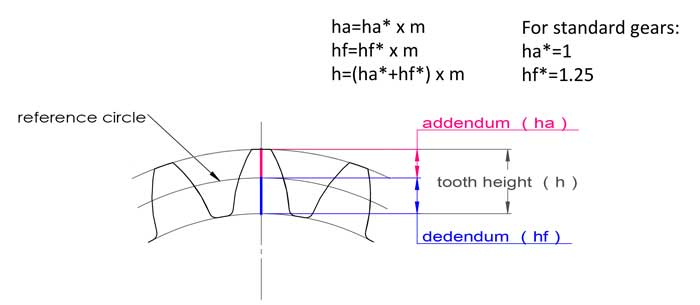
Il modulo ha anche a che fare con l'altezza del dente; per gli ingranaggi standard, l'altezza del dente è pari a 2,25*m:
addendum ha=1*m, dedendum hf=1,25*m, altezza del dente h=2,25*m.
4. Interasse (a)
2 ingranaggi hanno sempre lo stesso modulo, altrimenti non corrispondono. Ora possiamo concludere che a=(d1+d2)/2=m(z1+z2)/2, ma può essere leggermente diverso apportando alcune modifiche alle geometrie degli ingranaggi (spostamento del profilo dei denti).
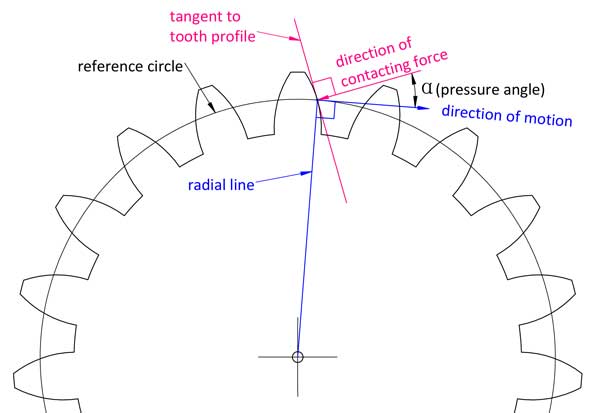
In parole povere, come suggerisce il nome, è l'angolo tra la direzione della forza di contatto sul punto di contatto del dente e la direzione del movimento di quel punto sul profilo del dente.
In geometria, è l'angolo tra la linea normale al profilo del dente involuto e la linea normale alla sua linea radiale.
Se si vuole comprendere appieno l'angolo di pressione, è necessario approfondire la comprensione della linea di rotazione del profilo del dente. Questa è solo una spiegazione più semplice.
Punti diversi del profilo del dente hanno angoli di pressione diversi, ma quando si parla dell'angolo di pressione di un ingranaggio, di solito ci si riferisce a quello sul cerchio di riferimento. La maggior parte degli ingranaggi utilizza 20° come angolo di pressione, alcuni sono a 14,5° o 25°. 2 ingranaggi accoppiati devono avere lo stesso modulo e lo stesso angolo di pressione.
6. Numero minimo di denti (zmin) senza sottotagliare la marcia
Non è possibile avere un numero di denti dell'ingranaggio a piacere. Se i denti sono troppo pochi, la parte inferiore dei denti si troverà al di sotto del punto limite; di conseguenza, quando i denti vengono realizzati con le frese, una parte in eccesso della radice dei denti verrà tagliata.
7. Coefficiente di spostamento del profilo (x)
Di solito per il profilo dei denti, l'addendum ha=1*m e il dedendum hf=1,25*m, tuttavia il profilo dei denti può essere spostato leggermente in alto o in basso:
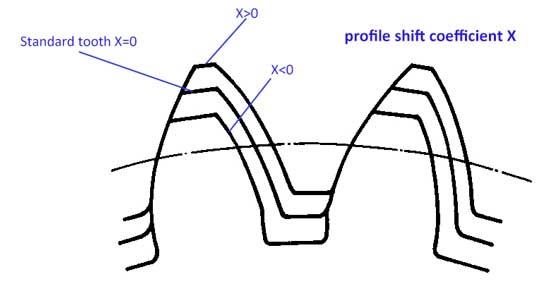

Ora abbiamo il coefficiente di spostamento del profilo (x). Quando il profilo viene spostato verso l'alto, il valore di x è positivo (x>0), mentre se il profilo viene spostato verso il basso, il valore di x è negativo (x<0).
Con lo spostamento del profilo dei denti, ora abbiamo:
- addendum ha=(1+x)*m
- deduzione hf=(1,25-x)*m
L'altezza del dente h=ha+hf=2,25*m è ancora uguale a quella dei denti standard.
Le ragioni principali dello spostamento del profilo sono:
1) Con il profilo spostato, possiamo evitare il sottosquadro dei denti con un numero inferiore di denti. La formula è la seguente:
xmin=(17-z)/17
Ad esempio, se si vuole che il numero di denti sia 14, allora X=(17-14)/17=0,176
2) Regolazione fine dell'interasse
a=[(m+x1)z1+(m+x2)z2]/2, quindi l'interasse non deve essere (z1+z2)*m
3) Rendere il pignone più robusto. Di solito il pignone si rompe prima dell'ingranaggio; aggiungendo un profilo positivo, la parte inferiore del pignone diventa più larga (mentre la punta si restringe), rendendolo così più resistente.
In sintesi:
| # | Articolo | Simbolo | Formula |
|---|---|---|---|
| 1 | numero di denti | z | |
| 2 | modulo | m | m=pitch/π |
| 3 | rapporto di trasmissione | i | i=d2/d1=z2/z1 1: ingranaggio motrice e 2: ingranaggio condotto. |
| 4 | coefficiente di addendum | da* | da*=1+x x=0 per le marce standard |
| 5 | coefficiente di deduzione | df* | df*=1,25-x |
| 6 | coefficiente di spostamento del profilo | x | Per gli ingranaggi standard, x=0 |
| 7 | angolo di pressione | α | α=20° per la maggior parte delle marce Altri meno utilizzati sono 14,5° e 25°. |
| 8 | diametro di riferimento | d | d=mz |
| 9 | diametro della punta | da | da=d+2Ha* x m, da=(z+2ha*) m Per gli ingranaggi standard, da=(z+2) x m |
| 10 | diametro delle radici | df | df=d-2Hf* x m, df=(z-2hf*) x m Per gli ingranaggi standard, df=(z-2,5) x m |
| 11 | addendum | ha | ha=m x ha* Per gli ingranaggi standard, ha=m |
| 12 | dedendum | hf | hf=m x hf* Per gli ingranaggi standard, hf=1,25m |
| 13 | altezza del dente | h | h=m x (ha*+hf*) ha*+Hf*=2,25 per la maggior parte delle marce |
| 14 | distanza dal centro | a | a=m x (z1+z2)/2 per ingranaggi standard a=[(m+x1)z1+(m+x2)z2]/2 per le marce spostate a profilo |
| 15 | Numero minimo di denti senza sottosquadro | Zmin | Zmin=2ha*/sinα^2 Zmin=17 quando ha*=1, α=20° |
| 16 | Minimo spostamento del profilo senza sottosquadro | Xmin | Xmin=(17-z)/17 |
Domande frequenti
Introduzione alle forze di trasmissione
Nel processo di ingranamento tra due ingranaggi, la forza esercitata dall'ingranaggio motore sull'ingranaggio condotto può essere scomposta in una forza normale perpendicolare alla superficie dell'ingranaggio condotto e in una forza tangenziale perpendicolare alla forza normale. La forza tangenziale non partecipa all'azionamento dell'ingranaggio condotto e causa l'usura tra i due ingranaggi. L'angolo nel punto di ingranamento dell'ingranaggio motore e di quello condotto è maggiore all'inizio e alla fine dell'ingranamento e minore al centro. Quando il punto di ingranamento si trova sulla linea centrale dei due ingranaggi, è uguale a zero. Pertanto, un angolo più piccolo può migliorare l'efficienza della trasmissione e ridurre l'usura.
Relazione tra angolo di pressione e angolo di retinatura
L'angolo di pressione è direttamente correlato all'angolo di ingranamento. D'altra parte, un angolo di pressione più piccolo comporta radici di ingranaggi più sottili, che riducono la resistenza degli ingranaggi. È quindi importante trovare un equilibrio.
Standard industriali per gli angoli di pressione degli ingranaggi
- Nella produzione industriale attuale, la maggior parte degli ingranaggi standard utilizza un angolo di pressione di 20°.
- Gli ingranaggi progettati per carichi leggeri e velocità elevate utilizzano spesso un angolo di pressione di 14,5°, che presenta i vantaggi di una minore rumorosità e di una maggiore efficienza di trasmissione.
- Gli ingranaggi progettati per applicazioni a bassa velocità e con carichi pesanti utilizzano un angolo di pressione di 25°, che offre una maggiore resistenza del dente, ma al costo di una minore efficienza della trasmissione e di una maggiore rumorosità.
Ingranaggi in plastica
Per gli ingranaggi in plastica è possibile scegliere qualsiasi angolo di pressione, poiché per la loro produzione non sono necessari utensili da taglio standard. Tuttavia, per semplicità di progettazione, è comune attenersi a questi valori standard.
La circonferenza del cerchio è la base per il calcolo degli ingranaggi. Il suo diametro è calcolato come il modulo (m) moltiplicato per il numero di denti (Z). In sostanza, si tratta di un cerchio teorico utilizzato principalmente per i calcoli, da cui derivano gli altri parametri degli ingranaggi.
Il diametro del passo, invece, viene definito durante l'ingranamento effettivo di due ingranaggi. È il cerchio formato dall'intersezione tra la normale comune degli ingranaggi e la linea che collega i loro centri, passando per il punto di tangenza. I cerchi del passo di due ingranaggi ingranati sono tangenti tra loro. Tuttavia, i cerchi della circonferenza potrebbero non essere sempre tangenti.
Nei modelli di ingranaggi standard, il cerchio della circonferenza e il cerchio del passo sono in genere sovrapposti. Tuttavia, se l'interasse viene regolato per aumentare il gioco o se gli ingranaggi sono stati modificati, il cerchio di circonferenza e il cerchio del passo possono differire.
Sì. Nei progetti standard, lo spessore del dente e la larghezza della scanalatura sul cerchio della circonferenza sono uguali.
Tuttavia, nelle applicazioni pratiche, per consentire un certo gioco pur mantenendo l'interasse standard, lo spessore del dente viene reso leggermente più sottile.
Un metodo consiste nel rendere lo spessore del dente leggermente inferiore alla larghezza della scanalatura sul cerchio della circonferenza.
Un altro metodo consiste nell'installare gli ingranaggi a un interasse leggermente superiore a quello standard.
L'entità del gioco richiesto dipende dalla precisione di fabbricazione degli ingranaggi; una maggiore precisione riduce la necessità di gioco.
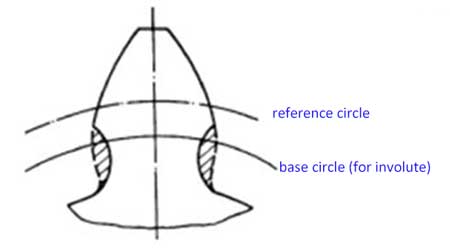
Il cerchio di base di un ingranaggio è il cerchio da cui si genera l'involucro. Il suo passo è la lunghezza dell'arco tra due punti identici dei profili di due denti adiacenti sul cerchio di base, quindi:
Pb = Db/Z.
Qui, Db è il diametro del cerchio di base.
Oppure Pb = Df * cos(α) / Z = mπ * cos(α),
dove Df è il diametro del cerchio di circonferenza, m è il modulo dell'ingranaggio e α è l'angolo di pressione del cerchio di circonferenza.
1. Per gli ingranaggi cilindrici, è necessario che l'ingranamento di una coppia di denti sia sincronizzato con quello della coppia precedente. Ciò richiede che i loro passi del cerchio di base siano uguali, il che significa:
m1 * cos(α1) = m2 * cos(α2).
Da ciò si deduce che i moduli (m) di una coppia di ingranaggi non devono necessariamente essere uguali.
2. Allo stesso tempo, il grado di ingranamento (rapporto di contatto ε) è maggiore di 1
Per gli ingranaggi prodotti con utensili da taglio standard, a causa della standardizzazione e della serializzazione degli utensili, è prassi comune utilizzare lo stesso modulo e lo stesso angolo di pressione del cerchio di circonferenza per entrambi gli ingranaggi.
3. Per gli ingranaggi elicoidali, è inoltre necessario che i loro angoli d'elica siano uguali, supponendo che i loro assi di montaggio siano paralleli.
Il rapporto di contatto (ε) è la lunghezza del segmento normale comune tra due ingranaggi ingranati, che è tagliato dai cerchi adduttori degli ingranaggi, diviso per il passo base (Pb) dell'ingranaggio.
- Quando ε <1, gli ingranaggi non possono funzionare correttamente perché ci sono momenti in cui nessun dente è in contatto.
- Se 1 < ε < 2, ci sono momenti in cui solo un dente è in contatto. Ad esempio, con ε = 1,63, si può immaginare una media di 1,63 coppie di denti che si ingranano. Durante 37% del processo di trasmissione, solo un dente è in contatto, mentre durante 63%, due denti sono in contatto, il che porta a un impatto maggiore durante la trasmissione.
- Se ε > 2, in qualsiasi momento, più di due coppie di denti sono in contatto e la trasmissione risulta più fluida.
Il numero di denti (Z) degli ingranaggi è un fattore importante che influenza il rapporto di contatto.
Per gli ingranaggi più piccoli, vengono spesso utilizzati ingranaggi elicoidali per aumentare il rapporto di contatto. Tuttavia, il costo di produzione degli ingranaggi elicoidali è notevolmente superiore a quello degli ingranaggi cilindrici.
Un altro metodo consiste nell'utilizzare un angolo di pressione minore del cerchio di lancio, ma questo ha un effetto minore.
La durata di vita di un ingranaggio è determinata principalmente dall'usura e dalla rottura per fatica. Questi problemi derivano da vari fattori, come la scarsa precisione dell'ingranaggio, il gioco inadeguato, la scarsa lubrificazione, il surriscaldamento e altro ancora. Sebbene sia difficile calcolare la durata di vita con formule empiriche, la precisione dell'ingranaggio e il materiale utilizzato sono fattori critici per la sua longevità.



I commenti sono chiusi.