Table des matières
ToggleVoici une version simplifiée de la terminologie des engrenages et des formules de calcul de la denture.
Ce billet a pour but d'expliquer la terminologie des engrenages et les formules de calcul de la denture d'une manière plus facile pour les débutants, ainsi que pour ceux qui ont appris les engrenages il y a longtemps mais qui veulent les reprendre rapidement.
Les engrenages ont de nombreux paramètres qui nécessitent un peu de mathématiques et de formation géométrique pour bien les comprendre. Cependant, vous n'avez pas besoin d'approfondir les concepts de base de la connaissance des engrenages, après avoir lu cet article, vous devriez être en mesure de faire des conceptions préliminaires d'engrenages ou d'avoir une communication efficace avec les concepteurs d'engrenages.
Commençons par la forme d'engrenage de base, les engrenages droits :
Table des matières
1. Nombre de dents (z) ; 2. Cercle de référence et diamètre de référence (d) ; 3. Module (m) ; 4. Distance du centre (a) ; 5.Angle de pression (α) ; 6. Nombre minimal de dents (zmin) ; 7. Coefficient de décalage du profil (x) ; 8. Tableau récapitulatif.
1. Nombre de dents (z)
C'est assez simple, il s'agit du nombre de dents de l'engrenage.
2. Cercle de référence et diamètre de référence (d)
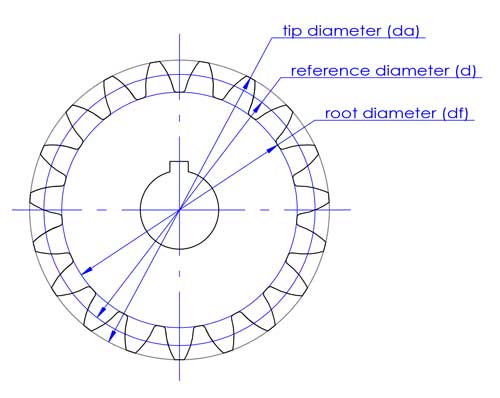
Le diamètre de la pointe (da) et le diamètre de la racine (df) correspondent au haut et au bas des dents.
Le diamètre de référence est utilisé dans la conception et le calcul des engrenages. Il est directement lié à d'autres paramètres importants de l'engrenage tels que le module (m), l'entraxe (c) et l'angle de pression (α).
Le diamètre de la pointe (da) et le diamètre de la racine (df) correspondent au haut et au bas des dents.
Le diamètre de référence est utilisé dans la conception et le calcul des engrenages. Il est directement lié à d'autres paramètres importants de l'engrenage tels que le module (m), l'entraxe (c) et l'angle de pression (α).
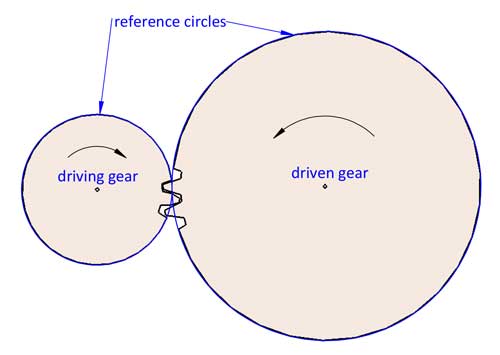
La rotation de deux engrenages peut être considérée comme une rotation engagée de deux cercles de référence sans glissement. Le rapport de transmission i=d2/d1. d1 et d2 sont les diamètres de référence de deux engrenages appariés (l'engrenage 1 est l'engrenage menant et l'engrenage 2 est l'engrenage mené).

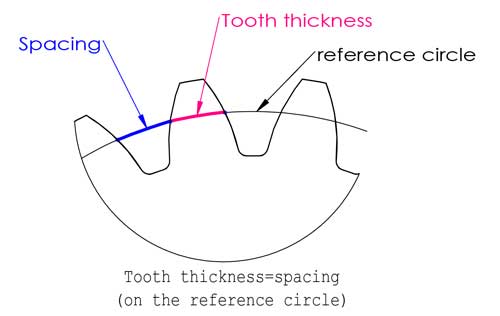
Le cercle de référence est situé quelque part entre la pointe et le bas des dents, généralement là où l'épaisseur de la dent est égale à l'espacement, mais ce n'est pas toujours le cas (nous parlerons du décalage de profil plus loin dans ce billet).
3. Module (m)
Le module est probablement le paramètre le plus important de l'engrenage, et il apparaît presque partout dans les formules de calcul de la denture. En fait, il n'est pas aussi difficile à comprendre qu'on pourrait l'imaginer. Le pas est la longueur de l'arc entre des points correspondants sur des dents adjacentes, généralement sur le cercle de référence.
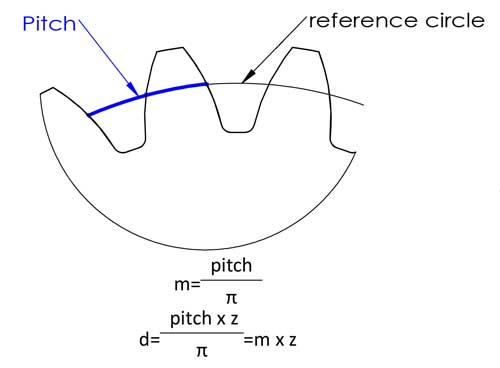

Ensuite, nous avons le diamètre de référence d=circonférence/π=pitch*z/π, pour faciliter le calcul, nous définissons le pitch/π comme le module, et maintenant nous avons l'équation de d=m*z, ce qui rend le calcul beaucoup plus facile, n'est-ce pas ? Les modules ont été normalisés selon les chiffres suivants (unité : mm) :
Première série (recommandée) : 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Deuxième série (moins utilisée) : 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Toutefois, pour les engrenages en plastique moulé par injection, il n'est pas nécessaire d'adopter ces numéros de modules standard, car les dents ne sont pas taillées par des fraises à dents standard.
Nous avons maintenant le rapport de transmission i=d2/d1=z2/z1 (la vitesse 1 est la vitesse motrice, et la vitesse 2 est la vitesse entraînée).
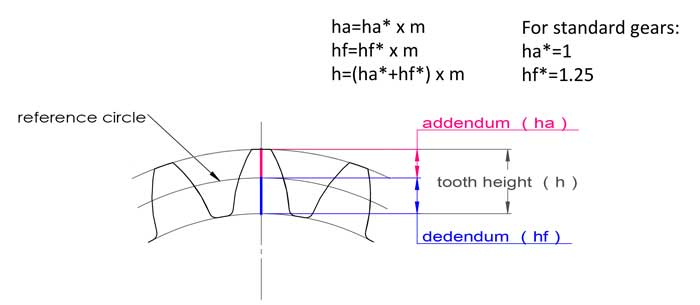
Le module est également lié à la hauteur de la dent. Pour les engrenages standard, la hauteur de la dent est égale à 2,25*m :
addendum ha=1*m, dedendum hf=1.25*m, hauteur de dent h=2.25*m.
4. Entraxe (a)
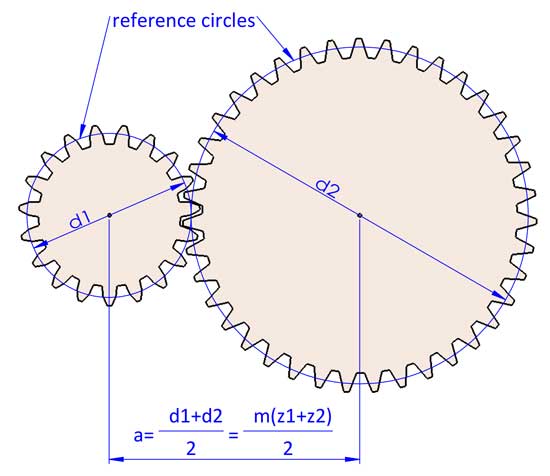
2 engrenages en prise ont toujours le même module, sinon ils ne correspondent pas. Nous pouvons maintenant conclure quea=(d1+d2)/2=m(z1+z2)/2, mais cela peut être légèrement différent en faisant quelques ajustements sur les géométries des engrenages (décalage du profil des dents).
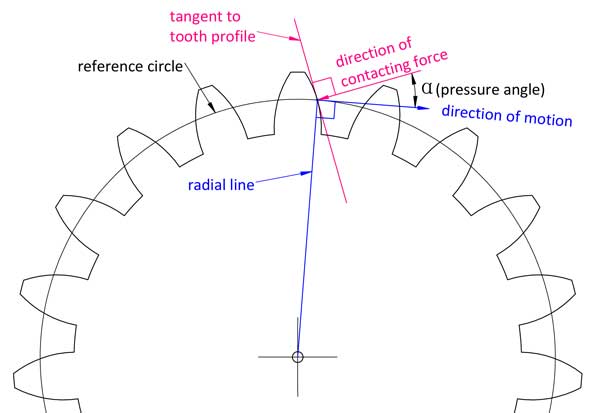
En termes simples, comme son nom l'indique, il s'agit de l'angle entre la direction de la force de contact sur le point de contact de la dent et la direction du mouvement de ce point sur le profil de la dent.
En géométrie, il s'agit de l'angle entre la ligne normale au profil de la dent en développante et la ligne normale à sa ligne radiale.
Pour bien comprendre l'angle de pression, il faut aller plus loin et comprendre la ligne d'inversion du profil de la dent. Il s'agit simplement d'une explication plus simple.
Différents points du profil de la dent ont des angles de pression différents, mais lorsque nous parlons de l'angle de pression d'un engrenage, il s'agit généralement de l'angle sur le cercle de référence. La plupart des engrenages utilisent un angle de pression de 20°, certains de 14,5° ou de 25°. 2 engrenages accouplés doivent avoir le même module et le même angle de pression.
6. Nombre minimal de dents (zmin) sans sous-cotation de l'engrenage
Le nombre de dents de l'engrenage ne peut pas être illimité. S'il y a trop peu de dents, le bas des dents sera en dessous du point limite, et par conséquent, lorsque les dents sont fabriquées par des fraises, une partie excédentaire de la racine des dents sera coupée.
7. Coefficient de décalage du profil (x)
En général, pour le profil des dents, l'addendum ha=1*m et le dedendum hf=1,25*m, mais le profil des dents peut être légèrement modifié vers le haut ou vers le bas :
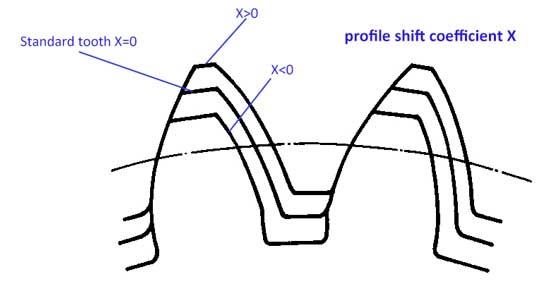

Nous avons maintenant le coefficient de déplacement du profil (x). Lorsque le profil est déplacé vers le haut, la valeur de x est positive (x>0), et si le profil est déplacé vers le bas, la valeur de x est négative (x<0).
Avec le déplacement du profil des dents, nous avons maintenant :
- addendum ha=(1+x)*m
- dedendum hf=(1.25-x)*m
La hauteur des dents h=ha+hf=2,25*m, reste identique à celle des dents standard.
Les principales raisons de ce changement de profil sont les suivantes :
1) Avec le profil décalé, nous pouvons éviter le sous-découpage des dents en réduisant le nombre de dents. La formule est la suivante :
xmin=(17-z)/17
Par exemple, si vous voulez que le nombre de dents soit de 14, X=(17-14)/17=0.176
2) Réglage précis de l'entraxe
a=[(m+x1)z1+(m+x2)z2]/2, donc la distance au centre ne doit pas être (z1+z2)*m
3) Renforcer le pignon. En ajoutant un changement de profil positif, le bas du pignon devient plus large (tandis que la pointe devient plus étroite), ce qui le rend plus solide.
En résumé :
| # | Objet | Symbole | Formule |
|---|---|---|---|
| 1 | nombre de dents | z | |
| 2 | module | m | m=pitch/π |
| 3 | rapport de démultiplication | i | i=d2/d1=z2/z1 1 : roue motrice, et 2 : roue entraînée |
| 4 | coefficient d'addition | da* | da*=1+x x=0 pour les engrenages standard |
| 5 | coefficient de dédommagement | df* | df*=1,25-x |
| 6 | coefficient de décalage du profil | x | Pour les engrenages standard, x=0 |
| 7 | angle de pression | α | α=20° pour la plupart des vitesses D'autres moins utilisés sont 14,5° et 25°. |
| 8 | diamètre de référence | d | d=mz |
| 9 | diamètre de la pointe | da | da=d+2Ha* x m, da=(z+2ha*) m Pour les engrenages standard, da=(z+2) x m |
| 10 | diamètre de la racine | df | df=d-2Hf* x m, df=(z-2hf*) x m Pour les engrenages standard, df=(z-2.5) x m |
| 11 | addendum | ha | ha=m x ha* Pour les engrenages standard, ha=m |
| 12 | dédommagement | hf | hf=m x hf* Pour les engrenages standard, hf=1,25m |
| 13 | hauteur de la dent | h | h=m x (ha*+hf*) ha*+Hf*=2,25 pour la plupart des vitesses |
| 14 | distance centrale | a | a=m x (z1+z2)/2 pour les engrenages standard a=[(m+x1)z1+(m+x2)z2]/2 pour les vitesses à profil décalé |
| 15 | Nombre minimal de dents sans contre-dépouille | Zmin | Zmin=2ha*/sinα^2 Zmin=17 lorsque ha*=1, α=20°. |
| 16 | Décalage minimal du profil sans contre-dépouille | Xmin | Xmin=(17-z)/17 |
Questions fréquemment posées
Introduction aux forces d'engrenage
Dans le processus d'engrènement entre deux engrenages, la force exercée par l'engrenage menant sur l'engrenage mené peut être décomposée en une force normale perpendiculaire à la surface de l'engrenage mené et une force tangentielle perpendiculaire à la force normale. La force tangentielle ne participe pas à l'entraînement de l'engrenage mené et provoque l'usure des deux engrenages. L'angle au point d'engrènement de la roue menante et de la roue menée est le plus grand au début et à la fin de l'engrènement et plus petit au milieu. Lorsque le point d'engrènement est situé sur la ligne médiane des deux engrenages, il est égal à zéro. Par conséquent, un angle plus faible peut améliorer l'efficacité de la transmission et réduire l'usure.
Relation entre l'angle de pression et l'angle de maillage
L'angle de pression est directement lié à l'angle d'engrènement. D'autre part, un angle de pression plus faible se traduit par des racines d'engrenage plus minces, ce qui réduit la résistance des engrenages. Il est donc important de trouver un équilibre.
Normes industrielles pour les angles de pression des engrenages
- Dans la production industrielle actuelle, la plupart des engrenages standard utilisent un angle de pression de 20°.
- Les engrenages conçus pour des charges légères et des vitesses élevées utilisent souvent un angle de pression de 14,5°, qui présente l'avantage de réduire le bruit et d'augmenter l'efficacité de la transmission.
- Les engrenages conçus pour les applications à faible vitesse et à forte charge utilisent un angle de pression de 25°, qui offre une plus grande résistance de la denture, mais au prix d'une efficacité de transmission plus faible et d'un niveau de bruit plus élevé.
Engrenages en plastique
Pour les engrenages en plastique, n'importe quel angle de pression peut être choisi puisque leur fabrication ne nécessite pas d'outils de coupe standard. Toutefois, pour des raisons de simplicité de conception, il est courant de s'en tenir à ces valeurs standard.
Le cercle de circonférence est la base du calcul des engrenages. Son diamètre est calculé en multipliant le module (m) par le nombre de dents (Z). Il s'agit essentiellement d'un cercle théorique utilisé principalement pour les calculs, les autres paramètres de l'engrenage étant dérivés de ce cercle.
Le diamètre primitif, quant à lui, est défini lors de l'engrènement de deux engrenages. Il s'agit du cercle formé par l'intersection de la normale commune des engrenages et de la ligne reliant leurs centres, en passant par le point de tangence. Les cercles primitifs de deux engrenages en prise sont tangents l'un à l'autre. Toutefois, les cercles de circonférence ne sont pas toujours tangents
Dans les modèles d'engrenages standard, le cercle de circonférence et le cercle primitif se chevauchent généralement. Toutefois, si l'entraxe est ajusté pour augmenter le jeu ou si les engrenages ont été modifiés, le cercle de circonférence et le cercle primitif peuvent différer.
Oui. Dans les modèles standard, l'épaisseur de la dent et la largeur de la fente sur le cercle de circonférence sont égales.
Cependant, dans les applications pratiques, pour permettre un certain jeu tout en conservant l'entraxe standard, l'épaisseur de la dent est légèrement réduite.
Une méthode consiste à faire en sorte que l'épaisseur de la dent soit légèrement inférieure à la largeur de la fente sur le cercle de circonférence.
Une autre méthode consiste à installer les engrenages à un entraxe légèrement supérieur à la norme.
L'importance du jeu dépend de la précision de fabrication des engrenages ; une plus grande précision réduit le besoin de jeu.
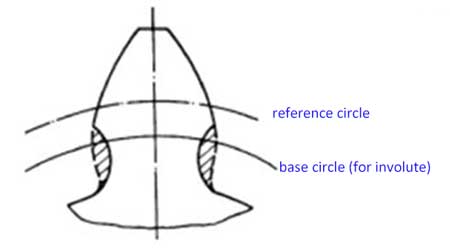
Le cercle de base d'un engrenage est le cercle à partir duquel sa développante est générée. Son pas est la longueur de l'arc entre des points identiques sur les profils de deux dents adjacentes sur le cercle de base :
Pb = Db/Z.
Ici, Db est le diamètre du cercle de base.
Ou Pb = Df * cos(α) / Z = mπ * cos(α),
où Df est le diamètre du cercle de circonférence, m est le module de l'engrenage, et α est l'angle de pression du cercle de circonférence.
1. Pour les engrenages droits, il est nécessaire que l'engrènement d'une paire de dents soit synchronisé avec l'engrènement de la paire précédente. Cela signifie que les pas de leurs cercles de base doivent être égaux :
m1 * cos(α1) = m2 * cos(α2).
On peut en déduire que les modules (m) d'une paire d'engrenages ne doivent pas nécessairement être égaux.
2. Dans le même temps, le degré d'engagement (rapport de contact ε) est supérieur à 1
Pour les engrenages fabriqués avec des outils de coupe standard, en raison de la normalisation et de la sérialisation des outils, il est courant d'utiliser le même module et le même angle de pression du cercle de circonférence pour les deux engrenages.
3. Pour les engrenages hélicoïdaux, il est également nécessaire que leurs angles d'hélice soient égaux, en supposant que leurs axes d'installation soient parallèles.
Le rapport de contact (ε) est la longueur du segment normal commun entre deux engrenages en prise, qui est coupé par les cercles d'addendum des engrenages, divisé par le pas de base (Pb) de l'engrenage.
- Lorsque ε <1, les engrenages ne peuvent pas fonctionner correctement car il y a des moments où aucune dent n'est en contact.
- Si 1 < ε < 2, il y a des moments où une seule dent est en contact. Par exemple, avec ε = 1,63, on peut imaginer une moyenne de 1,63 paires de dents en prise. Pendant 37% du processus de transmission, une seule dent est en prise, alors que pendant 63%, deux dents sont en prise, ce qui entraîne un impact plus important pendant la transmission.
- Si ε > 2, plus de deux paires de dents sont en contact à tout moment, ce qui permet une transmission plus douce.
Le nombre de dents (Z) sur les engrenages est un facteur important qui affecte le rapport de contact.
Pour les engrenages plus petits, les engrenages hélicoïdaux sont souvent utilisés pour augmenter le rapport de contact. Toutefois, le coût de fabrication des engrenages hélicoïdaux est nettement plus élevé que celui des engrenages droits.
Une autre méthode consiste à utiliser un angle de pression plus faible du cercle de tangage, mais cela n'a qu'un effet mineur.
La durée de vie d'un engrenage est principalement déterminée par l'usure et la rupture par fatigue. Ces problèmes découlent de divers facteurs tels qu'une faible précision de l'engrenage, un jeu inapproprié, une mauvaise lubrification, une surchauffe, etc. Bien qu'il soit difficile de calculer la durée de vie à l'aide de formules empiriques, la précision de l'engrenage et le matériau utilisé sont des facteurs critiques pour sa longévité.



Les commentaires sont fermés.