Índice
ToggleMedición de la longitud normal común en los métodos de inspección de engranajes
Cuando se habla de métodos de inspección de engranajes, la medición de la longitud de la línea normal común presenta una técnica sencilla y rentable ampliamente utilizada en la producción de engranajes e inspecciones de ingeniería inversa.
Este método, comparado con la medición tradicional del grosor de los dientes individuales, no sólo simplifica la operación, sino que también evita eficazmente los problemas relacionados con la deformación elástica local causada por el contacto puntual, mejorando así la precisión de las mediciones. Cuando se mide con calibres vernier de dientes de engranaje el grosor de los dientes, es esencial asegurarse de que los calibradores permanecen paralelos a la superficie del diente, lo que sin duda aumenta la dificultad de la medición. Además, aunque el uso de equipos CNC (Control Numérico por Ordenador) para la medición es preciso, también es costoso y el proceso es engorroso.
Este artículo comenzará introduciendo el concepto básico de la línea involuta, profundizando gradualmente en el concepto de normal común del engranaje. Al final de este artículo, deberías tener una comprensión completa del mismo y ser capaz de aplicar este conocimiento de manera efectiva en tu trabajo.
Concepto básico de involutivo
Introducción a Involute: comprensión simplificada y conocimientos básicos
La involuta, un concepto frecuentemente mencionado en matemáticas e ingeniería, puede entenderse a través de un sencillo experimento: imaginemos que tenemos una cuerda fina no elástica enrollada alrededor de un objeto circular (pensemos que es un círculo perfecto). Cuando empezamos a desenrollar lentamente esta cuerda manteniéndola tensa, la trayectoria que sigue el extremo de la cuerda forma lo que se denomina un involuto. En este proceso, el objeto circular se denomina “círculo base”, y la cuerda que se desenrolla se conoce como “línea generatriz”.”

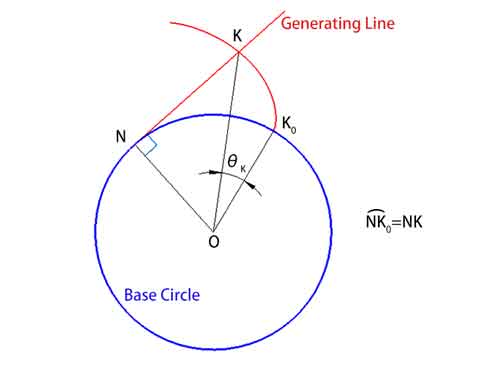
En esta acción, la línea generatriz permanece tangente a la circunferencia base, y en cualquier punto de la involuta, es perpendicular a la curva. Este ángulo, que llamamos ángulo de desenrollamiento θ (∠KOK0), es el ángulo que forma la recta que une el punto de la involuta (K) con el centro de la circunferencia base (O) desde el punto inicial de la involuta (K0) .
Cabe destacar que como la longitud de la cuerda no cambia, la longitud del arco en la circunferencia base (arco NK0) y la longitud de la línea generatriz (NK) son numéricamente iguales.
El concepto de ángulo de presión α y su variabilidad
Profundizando un poco más, vamos a hablar de un concepto estrechamente relacionado con la involuta: el ángulo de presión α. El ángulo de presión es el ángulo entre la normal en cualquier punto de la involuta (es decir, la línea perpendicular a la involuta) y la dirección de la velocidad a través de ese punto. Es importante tener en cuenta que el ángulo de presión varía en cada punto a lo largo de la involuta, partiendo de cero al principio de la involuta y aumentando gradualmente a medida que se desplaza hacia el exterior.
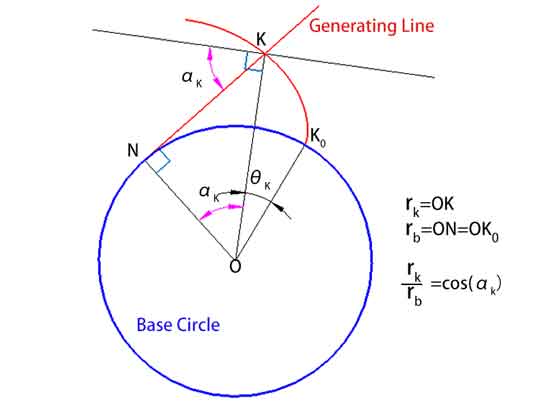
Además, la distancia desde un punto K de la involuta al centro del círculo, rk, puede calcularse mediante la fórmula rk = rb / cos(αk), donde rb es el radio del círculo base y αk es el ángulo de presión en el punto K.
Función normal común
La relación funcional entre el ángulo de desenrollado θ y el ángulo de presión α se denomina función involutiva, denotada por inv(α).
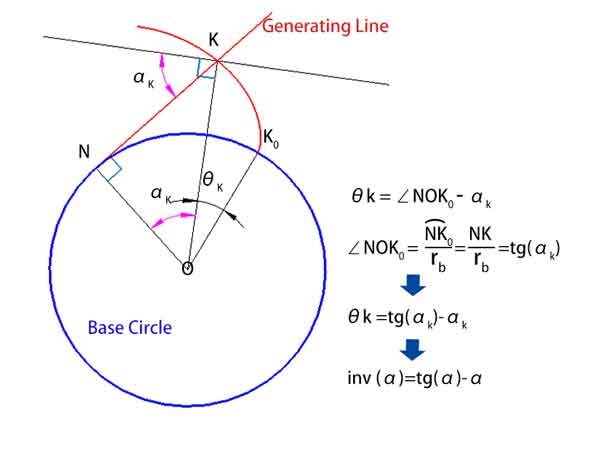
Como se muestra en el diagrama siguiente, θk = ∠NOK0 - αk.
Donde, el ∠NOK0 es igual a la longitud de arco NK0 dividida por el radio rb, medido en unidades de longitud de arco, que también pueden convertirse a grados.
Dado que la longitud de arco NK0 = NK, entonces = NK / rb = tg(αk).
Así, tenemos θk = tg(αk) - αk
Lo que significa inv(αk) = tg(αk) - αk
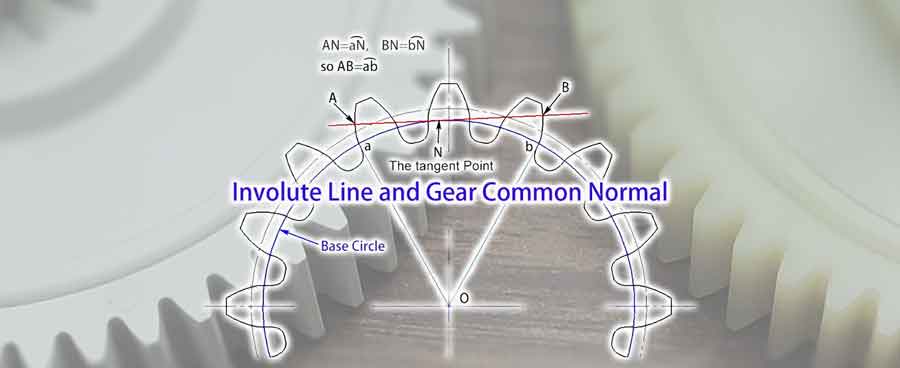
El concepto de normal común del engranaje
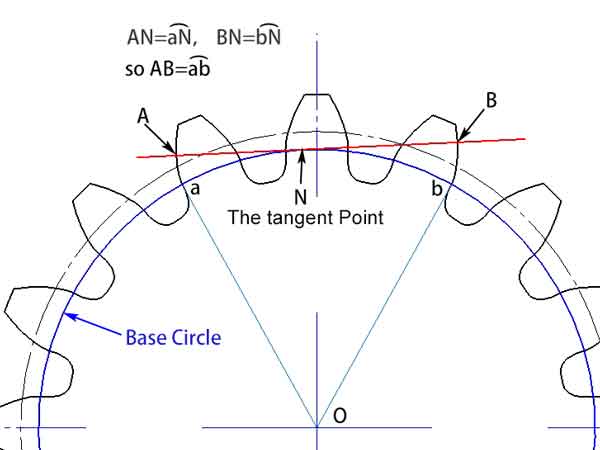
Una vez comprendido el concepto básico de involuta, podemos adentrarnos en el concepto de normal común del engranaje. Se refiere a cualquier línea tangente a la circunferencia base que incida a los perfiles del engranaje en puntos separados por varios dientes. Por las características de la involuta, sabemos que esta recta es perpendicular a las involutas que forman estos dos perfiles de engranaje, por lo que se denomina normal común.
A partir de las ilustraciones, podemos observar que la l longitud de la normal común (AB), situada entre estos dos perfiles de engranaje, es igual a la longitud de arcoab en el círculo base. Aunque cambie el ángulo de la normal común, su longitud permanece constante. Esta característica proporciona una ventaja significativa en las mediciones. Significa que incluso si hay alguna desviación en la posición de la herramienta de medición, no afectará al resultado de la medición.
número de diente
El número de dientes abarcados por la longitud normal común del engranaje se denomina “número de dientes abarcados” y puede determinarse a partir de la normal común dibujada en el plano. Existe una fórmula para calcularlo, pero el proceso de cálculo puede resultar algo engorroso, por lo que la observación directa a partir del plano resulta más sencilla y directa. La fórmula es:
k = zα / 180° + 0,5
Dónde:
kes el número de dientes abarcados,zes el número de dientes,αes el ángulo de presión del engranaje sobre el círculo de circunferencia, que es de 20° en la mayoría de los casosxes la marcha coeficiente de desplazamiento del perfil.
La longitud de la normal común también puede obtenerse a partir de dibujos CAD, pero también puede calcularse mediante una fórmula. Para ruedas dentadas con un coeficiente de modificación x = 0, la fórmula para calcular la distancia entre dientes es:
L = m cos α [(k - 0,5)π + z inv α]
Dónde:
Les la longitud de la normal común,αes el ángulo de presión en el círculo de referencia,kes el número de dientes abarcados.
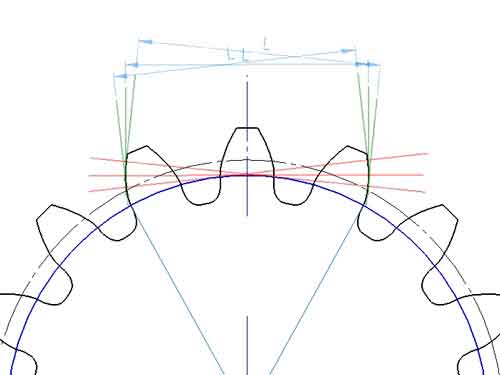
Las fórmulas mencionadas se calculan a partir del coeficiente de modificación x = 0, donde el espesor del diente en el círculo primitivo s = zm/2, que es la mitad del paso. Sin embargo, si x > 0, el espesor del diente en el círculo primitivo aumenta, lo que conduce a un aumento de L, y a la inversa, L disminuye si x < 0. Por lo tanto, la medición de la longitud de la normal común es un método eficaz para la ingeniería inversa de engranajes, que permite estimar el coeficiente de modificación del engranaje de muestra.
Conclusión
Para que este artículo sea conciso, no profundizaremos aquí en la derivación de estas fórmulas, que se tratarán en otros artículos.
Esperamos que este artículo le dé una idea clara de lo que es normal en común. Si tiene alguna duda, déjenos sus comentarios a continuación.