Inhaltsübersicht
Umschalten aufDies ist eine einfachere Version der Zahnradterminologie und der Berechnungsformeln für die Zähne
Dieser Beitrag soll Anfängern die Terminologie der Zahnräder und die Formeln zur Berechnung der Verzahnung erklären, aber auch denjenigen, die schon vor langer Zeit Zahnräder gelernt haben, aber schnell wieder einsteigen wollen.
Zahnräder haben viele Parameter, für deren vollständiges Verständnis ein wenig Mathematik und geometrische Kenntnisse erforderlich sind. Sie brauchen jedoch nicht zu tief in die grundlegenden Konzepte des Zahnradwissens einzusteigen. Nachdem Sie diesen Beitrag gelesen haben, sollten Sie in der Lage sein, vorläufige Zahnradentwürfe zu erstellen oder eine effektive Kommunikation mit Zahnradkonstrukteuren zu führen.
Beginnen wir mit der grundlegenden Zahnradform, den Stirnrädern:
Inhaltsübersicht
1. Anzahl der Zähne (z); 2. Referenzkreis und Referenzdurchmesser (d); 3. Modul (m); 4. Zentrumsabstand (a); 5.Eingriffswinkel (α); 6.Mindestzähnezahl (zmin); 7.Profilverschiebungskoeffizient (x); 8. Zusammenfassungstabelle.
1. Anzahl der Zähne (z)
Dies ist ziemlich einfach, es ist die Anzahl der Zähne des Zahnrads.
2. Bezugskreis und Bezugsdurchmesser (d)
Der Spitzendurchmesser (da) und der Wurzeldurchmesser (df) entsprechen dem oberen und unteren Ende der Zähne.
Der Bezugsdurchmesser wird bei der Auslegung und Berechnung von Zahnrädern verwendet. Er steht in direktem Zusammenhang mit anderen wichtigen Zahnradparametern wie dem Modul (m), dem Achsabstand (c) und dem Eingriffswinkel (α).
Der Spitzendurchmesser (da) und der Wurzeldurchmesser (df) entsprechen dem oberen und unteren Ende der Zähne.
Der Bezugsdurchmesser wird bei der Auslegung und Berechnung von Zahnrädern verwendet. Er steht in direktem Zusammenhang mit anderen wichtigen Zahnradparametern wie dem Modul (m), dem Achsabstand (c) und dem Eingriffswinkel (α).
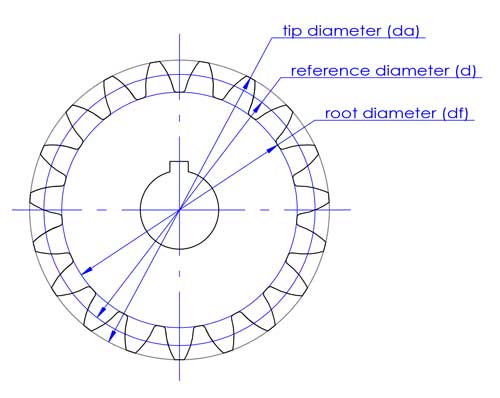
Die Drehung von 2 Zahnrädern kann als eingreifende Drehung von 2 Teilkreisen ohne Schlupf betrachtet werden. Das Übersetzungsverhältnis i=d2/d1. d1 und d2 beziehen sich auf die Bezugsdurchmesser von 2 ineinandergreifenden Zahnrädern (Rad 1 ist das treibende Rad und Rad 2 ist das getriebene Rad).
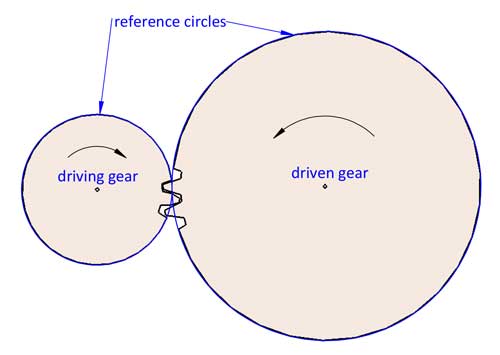

Der Referenzkreis befindet sich irgendwo zwischen der Spitze und der Unterseite der Zähne, normalerweise dort, wo die Zahndicke dem Abstand entspricht, aber das ist nicht immer der Fall (wir werden später in diesem Beitrag über Profilverschiebung sprechen).
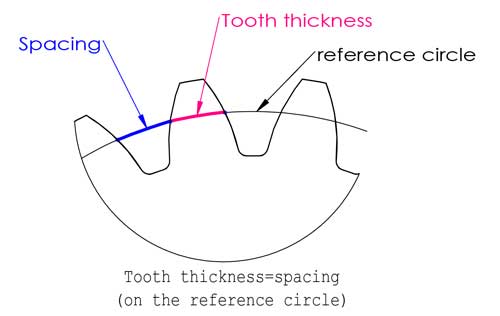
3. Modul (m)
Der Modul ist wahrscheinlich der wichtigste Zahnradparameter und taucht fast überall in den Formeln für die Zahnradberechnung auf. Eigentlich ist er gar nicht so schwer zu verstehen, wie Sie vielleicht denken. Zunächst wollen wir verstehen, was die Teilung ist. Die Teilung ist die Bogenlänge zwischen entsprechenden Punkten auf benachbarten Zähnen, normalerweise auf dem Bezugskreis.
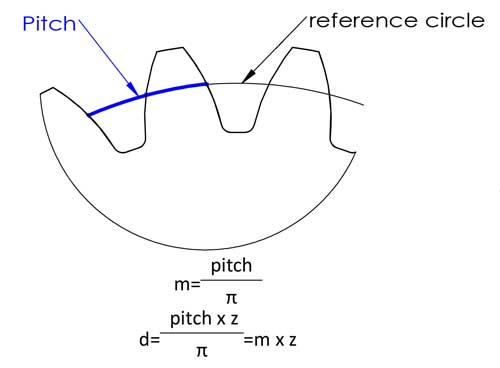

Dann haben wir den Bezugsdurchmesser d=Umfang/π=Teilung*z/π, um die Berechnung zu erleichtern, definieren wir die Teilung/π als Modul, und jetzt haben wir die Gleichung von d=m*z, das macht die Berechnung viel einfacher, oder? Die Module sind in folgenden Zahlen genormt (Einheit: mm):
Erste Serie (empfohlen): 0.1, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Zweite Serie (weniger verwendet): 0.35, 0.7, 0.9, 1.75, 2.25, 2.75, 3.25, 3.5, 3.75, 4.5, 5.5, 6.5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Bei spritzgegossenen Kunststoffzahnrädern besteht jedoch keine Notwendigkeit, diese Standardmodulnummern zu übernehmen, da die Zähne nicht mit Standardzahnfräsern geschnitten werden.
Jetzt haben wir das Übersetzungsverhältnis i=d2/d1=z2/z1 (Rad 1 ist das treibende Rad und Rad 2 ist das getriebene Rad).
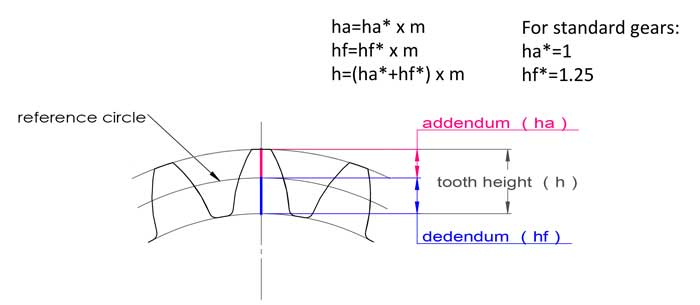
Das Modul hat auch mit der Zahnhöhe zu tun, bei Standardzahnrädern ist die Zahnhöhe gleich 2,25*m:
Kopfhöhe ha=1*m, Fußhöhe hf=1,25*m, Zahnhöhe h=2,25*m.
4. Achsabstand (a)
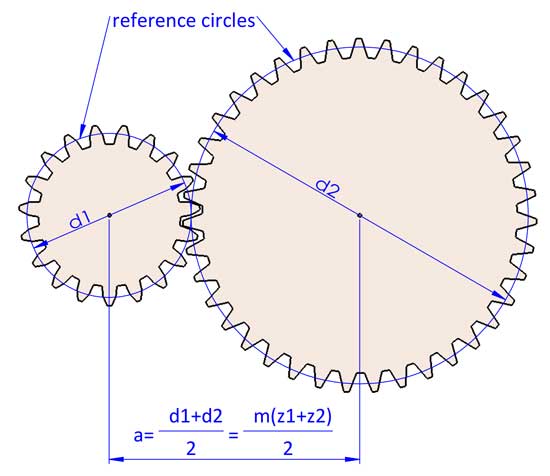
2 ineinander greifende Zahnräder haben immer den gleichen Modul, sonst passen sie nicht zusammen. Jetzt können wir zu dem Schluss kommen, dass a=(d1+d2)/2=m(z1+z2)/2, aber es kann etwas anders sein, wenn wir einige Anpassungen an den Zahnradgeometrien vornehmen (Verschiebung des Zahnprofils).
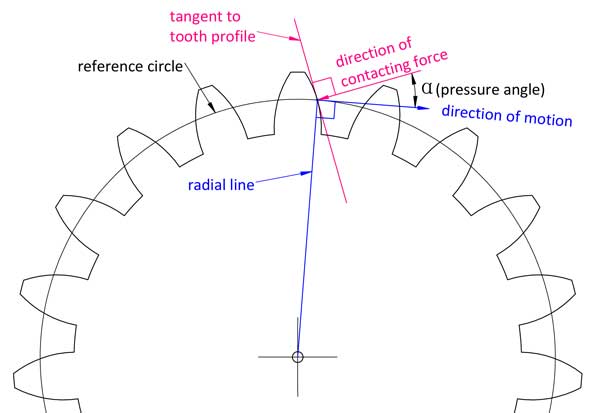
Wie der Name schon sagt, handelt es sich um den Winkel zwischen der Richtung der Kontaktkraft auf den Kontaktpunkt des Zahns und der Bewegungsrichtung dieses Punkts auf dem Zahnprofil.
In der Geometrie ist es der Winkel zwischen der Senkrechten auf das Evolventenprofil und der Senkrechten auf seine Radiallinie.
Wenn Sie den Eingriffswinkel vollständig verstehen wollen, müssen Sie tiefer gehen, um die Involutlinie des Zahnprofils zu verstehen. Dies ist nur eine einfachere Art der Erklärung.
Verschiedene Punkte auf dem Zahnprofil haben unterschiedliche Eingriffswinkel, aber wenn wir über den Eingriffswinkel eines Zahnrads sprechen, bezieht er sich in der Regel auf denjenigen auf dem Bezugskreis. Die meisten Zahnräder haben einen Eingriffswinkel von 20°, einige haben 14,5° oder 25°. 2 zueinander passende Zahnräder müssen den gleichen Modul und Eingriffswinkel haben.
6. Mindestzähnezahl (zmin) ohne Unterschneidung im Getriebe
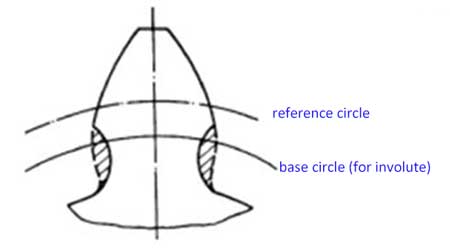
Die Zähnezahl des Zahnrads kann nicht beliebig sein. Wenn zu wenige Zähne vorhanden sind, liegt der untere Teil der Zähne unterhalb des Grenzpunktes, was zur Folge hat, dass bei der Herstellung der Zähne mit Zahnfräsern ein überschüssiger Teil des Zahnfußes abgeschnitten wird.
7. Profilverschiebungskoeffizient (x)
Normalerweise gilt für das Zahnprofil, dass der Zahnkopf ha=1*m und der Zahnfuß hf=1,25*m ist, jedoch kann das Zahnprofil ein wenig nach oben oder unten verschoben werden:
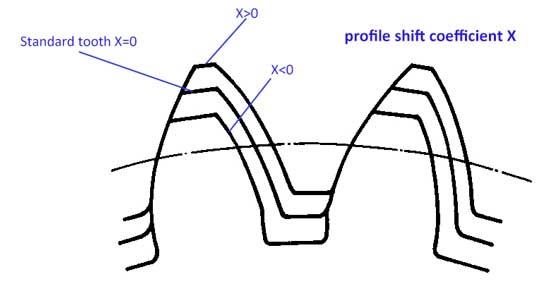

Jetzt haben wir den Profilverschiebungskoeffizienten (x). Wenn das Profil nach oben verschoben wird, ist der Wert von x positiv (x>0), und wenn das Profil nach unten verschoben wird, ist der Wert von x negativ (x<0).
Mit der Bewegung der Zähne Profil, jetzt haben wir:
- Nachtrag ha=(1+x)*m
- Ableitung hf=(1,25-x)*m
Zahnhöhe h=ha+hf=2,25*m, das ist immer noch dasselbe wie bei den Standardzähnen.
Die Hauptgründe für die Profilverschiebung sind:
1) Mit einem verschobenen Profil können wir die Unterschneidung der Zähne mit einer geringeren Anzahl von Zähnen vermeiden. Die Formel lautet wie folgt:
xmin=(17-z)/17
Wenn Sie zum Beispiel wollen, dass die Anzahl der Zähne 14 beträgt, dann ist X=(17-14)/17=0,176
2) Feinabstimmung des Achsabstands
a=[(m+x1)z1+(m+x2)z2]/2, also muss der Achsabstand nicht (z1+z2)*m sein
3) Verstärken Sie das Ritzel. Normalerweise versagt das Ritzel vor dem Zahnrad, durch das Hinzufügen einer positiven Profilverschiebung wird der Boden des Ritzels breiter (während die Spitze schmaler wird), wodurch es stärker wird.
Zusammengefasst:
| # | Artikel | Symbol | Formel |
|---|---|---|---|
| 1 | Zähnezahl | z | |
| 2 | Modul | m | m=Neigung/π |
| 3 | Getriebeübersetzung | i | i=d2/d1=z2/z1 1: Antriebsrad und 2: Abtriebsrad |
| 4 | Addendumskoeffizient | da* | da*=1+x x=0 für Standard-Getriebe |
| 5 | Dedendumskoeffizient | df* | df*=1,25-x |
| 6 | Profilverschiebungskoeffizient | x | Für Standard-Getriebe,, x=0 |
| 7 | Eingriffswinkel | α | α=20° für die meisten Zahnräder Andere, weniger verbreitete, sind 14,5° und 25°. |
| 8 | Referenzdurchmesser | d | d=mz |
| 9 | Durchmesser der Spitze | da | da=d+2Ha* x m, da=(z+2ha*) m Für Standard-Getriebe, da=(z+2) x m |
| 10 | Wurzeldurchmesser | df | df=d-2Hf* x m, df=(z-2hf*) x m Für Standard-Getriebe: df=(z-2,5) x m |
| 11 | Nachtrag | ha | ha=m x ha* Bei Standard-Getrieben ist ha=m |
| 12 | Dedendum | hf | hf=m x hf* Für Standard-Getriebe, hf=1,25m |
| 13 | Zahnhöhe | h | h=m x (ha*+hf*) ha*+Hf*=2,25 für die meisten Gänge |
| 14 | Achsabstand | a | a=m x (z1+z2)/2 für Standard-Getriebe a=[(m+x1)z1+(m+x2)z2]/2 für profilgeschaltete Zahnräder |
| 15 | Minimale Zähnezahl ohne Unterschneidung | Zmin | Zmin=2ha*/sinα^2 Zmin=17 wenn ha*=1, α=20° |
| 16 | Minimale Profilverschiebung ohne Unterschneidung | Xmin | Xmin=(17-z)/17 |
Häufig gestellte Fragen
Einführung in die Verzahnungskräfte
Beim Zahneingriff zwischen zwei Zahnrädern kann die Kraft, die das treibende Zahnrad auf das getriebene Zahnrad ausübt, in eine Normalkraft senkrecht zur Oberfläche des getriebenen Zahnrads und eine Tangentialkraft senkrecht zur Normalkraft zerlegt werden. Die Tangentialkraft trägt nicht zum Antrieb des angetriebenen Rades bei und verursacht Verschleiß zwischen den beiden Rädern. Der Winkel am Eingriffspunkt des treibenden und des getriebenen Zahnrads ist am Anfang und am Ende des Eingriffs am größten und in der Mitte am kleinsten. Wenn der Eingriffspunkt auf der Mittellinie der beiden Zahnräder liegt, ist er gleich Null. Daher kann ein kleinerer Winkel die Übertragungseffizienz verbessern und den Verschleiß verringern.
Verhältnis zwischen Eingriffswinkel und Maschenwinkel
Der Eingriffswinkel steht in direktem Zusammenhang mit dem Verzahnungswinkel. Andererseits führt ein kleinerer Eingriffswinkel zu dünneren Zahnradwurzeln, was die Festigkeit des Zahnrads verringert. Daher ist es wichtig, ein Gleichgewicht zu finden.
Industrielle Normen für Eingriffswinkel von Zahnrädern
- In der heutigen industriellen Produktion wird bei den meisten Standardgetrieben ein Eingriffswinkel von 20° verwendet.
- Bei Getrieben, die für leichte Lasten und hohe Drehzahlen ausgelegt sind, wird häufig ein Eingriffswinkel von 14,5° verwendet, der die Vorteile eines geringeren Geräuschpegels und eines höheren Wirkungsgrads der Übertragung hat.
- Bei Zahnrädern, die für niedrige Drehzahlen und schwere Lasten ausgelegt sind, wird ein Eingriffswinkel von 25° verwendet, der eine höhere Zahnfestigkeit bietet, jedoch auf Kosten eines geringeren Übertragungswirkungsgrads und einer höheren Geräuschentwicklung.
Kunststoffzahnräder
Für Kunststoffzahnräder kann jeder beliebige Eingriffswinkel gewählt werden, da für ihre Herstellung keine Standardschneidwerkzeuge erforderlich sind. Zur Vereinfachung der Konstruktion ist es jedoch üblich, sich an diese Standardwerte zu halten.
Der Umfangskreis ist die Grundlage für die Zahnradberechnung. Sein Durchmesser errechnet sich aus dem Modul (m) multipliziert mit der Anzahl der Zähne (Z). Im Wesentlichen handelt es sich um einen theoretischen Kreis, der vor allem für Berechnungen verwendet wird und von dem andere Verzahnungsparameter abgeleitet werden.
Der Teilkreisdurchmesser hingegen wird während des tatsächlichen Eingriffs zweier Zahnräder definiert. Er ist der Kreis, der durch den Schnittpunkt der gemeinsamen Normalen der Zahnräder mit der Verbindungslinie zwischen ihren Mittelpunkten gebildet wird und durch den Tangentenpunkt verläuft. Die Teilkreise von zwei ineinander greifenden Zahnrädern sind tangential zueinander. Die Umfangskreise müssen jedoch nicht immer tangential sein
Bei Standardzahnradkonstruktionen überschneiden sich Umfangskreis und Teilkreis normalerweise. Wenn jedoch der Achsabstand angepasst wird, um das Spiel zu vergrößern, oder wenn die Zahnräder modifiziert wurden, können der Umfangskreis und der Teilkreis voneinander abweichen.
Ja. Bei Standardkonstruktionen sind Zahndicke und Schlitzbreite auf dem Umfangskreis gleich.
In der Praxis wird die Zahndicke jedoch etwas dünner ausgeführt, um ein gewisses Spiel zu ermöglichen und gleichzeitig den Standard-Achsabstand beizubehalten.
Eine Methode besteht darin, die Zahndicke etwas kleiner zu machen als die Schlitzbreite auf dem Umfangskreis.
Eine andere Methode besteht darin, die Zahnräder mit einem etwas größeren Achsabstand als der Norm einzubauen.
Die erforderliche Größe des Spiels hängt von der Fertigungspräzision der Zahnräder ab; eine höhere Präzision verringert den Bedarf an Spiel.
Der Grundkreis eines Zahnrads ist der Kreis, aus dem seine Evolvente erzeugt wird. Seine Teilung ist die Bogenlänge zwischen identischen Punkten auf den Profilen zweier benachbarter Zähne auf dem Grundkreis, also:
Pb = Db/Z.
Dabei ist Db der Durchmesser des Grundkreises.
Oder Pb = Df * cos(α) / Z = mπ * cos(α),
wobei Df der Durchmesser des Umfangskreises, m der Modul des Zahnrads und α der Eingriffswinkel des Umfangskreises ist.
1. Bei Stirnrädern ist es erforderlich, dass der Eingriff eines Zahnpaares mit dem Eingriff des vorherigen Zahnpaares synchronisiert ist. Dies erfordert, dass ihre Grundkreisteilungen gleich sind, d.h.:
m1 * cos(α1) = m2 * cos(α2).
Daraus lässt sich ableiten, dass die Module (m) eines Paares von ineinander greifenden Zahnrädern nicht unbedingt gleich sein müssen.
2. Gleichzeitig ist der Grad des Eingriffs (Kontaktverhältnis ε) größer als 1
Bei Zahnrädern, die mit Standardschneidwerkzeugen hergestellt werden, ist es aufgrund der Standardisierung und Serialisierung der Werkzeuge üblich, für beide Zahnräder das gleiche Modul und den gleichen Eingriffswinkel des Umfangskreises zu verwenden.
3. Bei schrägverzahnten Zahnrädern müssen auch die Schrägungswinkel gleich sein, vorausgesetzt, die Montageachsen sind parallel.
Das Überdeckungsverhältnis (ε) ist die Länge des gemeinsamen Normalsegments zwischen zwei ineinandergreifenden Zahnrädern, das durch die Kopfkreise der Zahnräder geschnitten wird, geteilt durch die Grundteilung (Pb) des Zahnrads.
- Wenn ε <1 ist, können die Zahnräder nicht richtig funktionieren, weil es Momente gibt, in denen keine Zähne in Kontakt sind.
- Wenn 1 < ε < 2, gibt es Zeiten, in denen nur ein Zahn in Kontakt ist. Bei ε = 1,63 kann man sich zum Beispiel vorstellen, dass im Durchschnitt 1,63 Zahnpaare ineinander greifen. Bei 37% des Übertragungsvorgangs ist nur ein Zahn im Eingriff, während bei 63% zwei Zähne im Eingriff sind, was zu einer größeren Wirkung bei der Übertragung führt.
- Wenn ε > 2 ist, sind zu jedem Zeitpunkt mehr als zwei Zahnpaare in Kontakt, was zu einer gleichmäßigeren Übertragung führt.
Die Anzahl der Zähne (Z) auf den Zahnrädern ist ein wichtiger Faktor, der sich auf das Übersetzungsverhältnis auswirkt.
Bei kleineren Zahnrädern werden häufig schrägverzahnte Zahnräder verwendet, um das Übersetzungsverhältnis zu erhöhen. Allerdings sind die Herstellungskosten für schrägverzahnte Zahnräder deutlich höher als die von Stirnrädern.
Eine andere Methode besteht darin, einen kleineren Eingriffswinkel des Teilkreises zu verwenden, was jedoch nur eine geringe Wirkung hat.
Die Lebensdauer eines Zahnrads wird hauptsächlich durch Verschleiß und Ermüdungsbruch bestimmt. Diese Probleme sind auf verschiedene Faktoren zurückzuführen, wie z. B. eine geringe Präzision des Zahnrads, ein ungeeignetes Spiel, schlechte Schmierung, Überhitzung und vieles mehr. Es ist zwar schwierig, die Lebensdauer mit empirischen Formeln zu berechnen, aber die Präzision des Zahnrads und das verwendete Material sind entscheidende Faktoren für seine Langlebigkeit.



Die Kommentare sind geschlossen.